Коллоидная химия: Лабораторный практикум, страница 20

Для вычисления соотношения между работой адгезии и поверхностным натяжением представим взаимно нерастворимые жидкость и твердое тело, имеющие поверхности на границе с воздухом, равные единице площади. При контакте этих поверхностей происходит адгезия, но система остаётся трёхфазной, и возникает поверхностное натяжение, равное s_тж. Энергия Гиббса системы уменьшается на величину, равную работе адгезии, то есть                       DG = s_тж - (s_тг + s_жг),

С учетом (6.1), получаем уравнение Дюпре

W_a = s_жг + (s_тг - s_тж)                                            (6.2)

Это уравнение отражает закон сохранения энергии при адгезии. Из уравнения Дюпре следует, что работа адгезии тем больше, чем меньше поверхностное натяжение исходных компонентов, и тем меньше, чем больше межфазное натяжение s_тж. Межмолекулярные взаимодействия внутри фазы называется когезией. В случае нарушения когезионной целостности жидкости в воздушной среде работа когезии равна W_к = s_жг.

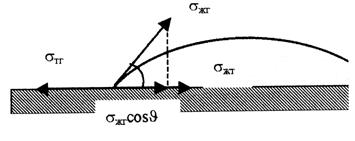
Работу адгезии можно определить, зная количественную характеристику смачивания, а именно краевой угол смачивания q. Рассмотрим положение капли жидкости на твердой поверхности (рис. 6.2). В каждой точке динии смачивания (то есть окружности капли) имеется контакт трех фаз: твердой, жидкой и газообразной. Разграничивающие их поверхности твердое тело - жидкость, твердое тело - газ и жидкость - газ имеют соответственно межфазное поверхностное натяжение s_тж, s_тг и s_жг.

С другой стороны поверхностное натяжение можно представить как силу, действующую на единицу длины линии, вдоль которой соприкасаются три фазы. Вектор силы поверхностного натяжения s_тг направлен таким образом, чтобы уменьшить поверхность раздела твердой и газообразной фаз, то есть растянуть каплю; вектор межфазного натяжения s_тж действует в противополож­ном направлении и стремится сократить площадь контакта жидкость - твердое тело; вектор поверхностного натяжения s_жг направлен так, чтобы придать капле форму, отвечающую минимальной площади поверхности раздела фаз. Таким образом, в любой точке линии смачивания действуют три силы s_тж, s_тг и s_жг (рис.6.2), направленные нормально к линии смачивания и тангенциально к соответствующей поверхности раздела фаз. В состоянии равновесия соотношение этих сил выражается уравнением Юнга:

s_тж = s_тг + s_жг×cosq,

или                                                     s_тж - s_тг = s_жг×cosq,                                               (6.3)

где q - краевой угол смачивания, отсчитываемый так, чтобы жидкость находилась внутри угла. Подставив значение (s_тж - s_тг) из уравнения (6.3) в уравнение (6.2), получим выражение, называемое уравнением Дюпре - Юнга для работы равновесной адгезии

W_A = s_жг(1 + cosq),           (6.4)

или          

Следовательно, чем больше разность между работой адгезии и работой когезии или между работой адгезии и поверхностным натяжением s_жг, тем лучше жидкость смачивает поверхность. Так углеводороды, поверхностное натяжение которых на границе с воздухом составляет (17 - 25)×10^-3 Дж/м², смачивают практически любые твердые поверхности. Вода, поверхностное натяжение которой на границе с воздухом составляет 72,75 ×10^-3 Дж/м² (при 20°С), хорошо смачивает стекло, кварц, карбонаты, сульфаты, многие силикаты. Некоторые твердые вещества, в частности графит и тальк, смачиваются на границе с воздухом (q < 90°) как неполярными жидкостями, так и водой. При конкурентном смачивании поверхности водой в присутствии жидкого углеводорода, если вода образует острый краевой угол с твердой поверхностью (q < 90°), то поверхность называют гидрофильной или олеофобной, если неполярная жидкость вытесняет воду с поверхности и для воды краевой угол q >90°, то поверхность называют гидрофобной или олеофильной.