На следующей стадии
необходимо найти касательную к построенной кривой при заданном х. Графическое
определение касательной – это прямая, представляющая предельное положение
секущей, при котором длина отсекаемой дуги равна нулю. Рисунок П2.2
иллюстрирует это определение на примере окружности (рис. а) и произвольной
(дифференцируемой) кривой (рис. б). Пусть дана точка А на окружно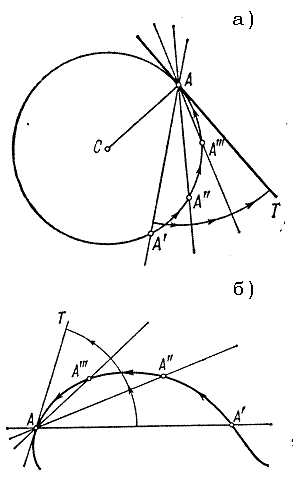 сти (рис. а). Выберем
любую другую точку на окружности А' и соединим её с А секущей АА'. Пусть точка
А' движется по окружности в направлении уменьшения длины отсекаемой дуги через
последовательные положения A'', А''', … Очевидно, что в пределе секущая займёт
такое положение АТ, при котором она будет иметь только одну общую точку с
окружностью, именно точку А. В таком положении она называется касательной.
сти (рис. а). Выберем
любую другую точку на окружности А' и соединим её с А секущей АА'. Пусть точка
А' движется по окружности в направлении уменьшения длины отсекаемой дуги через
последовательные положения A'', А''', … Очевидно, что в пределе секущая займёт
такое положение АТ, при котором она будет иметь только одну общую точку с
окружностью, именно точку А. В таком положении она называется касательной.
Это определение можно использовать практически для нахождения касательной в точке А. Для этого следует положить линейку так чтобы она проходила через точку А и произвольную точку А', и поворачивать её вокруг А до положения АТ. (Чтобы линейка не смещалась от точки А при движении, можно воткнуть булавку рядом с этой точкой и слегка опираться на неё краем линейки).
 Другой метод
построения касательной показан на рис. П2.3. На выбранном отрезке кривой
проводят две параллельные хорды АВ и A'B'. Делят их пополам и через полученные
середины проводят прямую EF, пересекающую кривую в точке О. Прямая CD, проведённая
через найденную точку О параллельно хордам АВ и A'B', является касательной к
кривой в точке О. Следует обратить внимание, что в этом методе мы не задаёмся
заранее точкой О, через которую должна быть проведена касательная, а находим её
путём построений. Предварительно мы задаёмся только дугой АОВ, в пределах
которой эта точка оказывается. Мы делаем это неявно проведением хорды АВ.
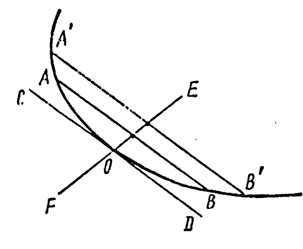
Другой метод
построения касательной показан на рис. П2.3. На выбранном отрезке кривой
проводят две параллельные хорды АВ и A'B'. Делят их пополам и через полученные
середины проводят прямую EF, пересекающую кривую в точке О. Прямая CD, проведённая
через найденную точку О параллельно хордам АВ и A'B', является касательной к
кривой в точке О. Следует обратить внимание, что в этом методе мы не задаёмся
заранее точкой О, через которую должна быть проведена касательная, а находим её
путём построений. Предварительно мы задаёмся только дугой АОВ, в пределах
которой эта точка оказывается. Мы делаем это неявно проведением хорды АВ.

 Описанные два метода
построения эффективны только в тех случаях, когда точка касания находится на
участке кривой, на котором кривизна является приблизительно постоянной, или,
проще говоря, когда этот участок похож по своей форме на дугу окружности.
Описанные два метода
построения эффективны только в тех случаях, когда точка касания находится на
участке кривой, на котором кривизна является приблизительно постоянной, или,
проще говоря, когда этот участок похож по своей форме на дугу окружности.
Единственным универсальным и действительно надёжным является метод прямоугольного зеркала. Такое зеркальце ставят ребром поперёк кривой так, чтобы его край с отражающей стороны проходил через заданную точку касания. Затем его поворачивают вокруг этой точки до положения, при котором отражение в зеркале выглядит продолжением (без излома) отрезка кривой, расположенного перед зеркалом. Когда такое положение найдено, отмечают след зеркала, проведя прямую по его краю. Затем зеркало отнимают и проводят прямую, проходящую через заданную точку перпендикулярно следу зеркала. Эта последняя прямая является касательной.
Производная функции у = ¦(х) в точке касания равна по определению коэффициенту наклона касательной. Этот коэффициент находят так же, как угловой коэффициент линейного графика (см. выше приложение 2.1). То есть, чтобы найти его графическим методом, нужно отвлечься от нелинейного графика у = ¦(х) и от точки касания на нём, и рассматривать построенную касательную как отдельный линейный график.
2.3 Графическая экстраполяция
Пусть даны пары чисел (xi , yi ), i = 1, 2, 3, …N, которые отвечают неизвестной функциональной зависимости y = ¦(x). Предположим, требуется найти приближённое значение у для некоторого х, не равного ни одному из данных xi. Мы можем применить для этого какую-нибудь вычислительную или графическую процедуру. Например, можно построить диаграмму рассеяния в координатах (х, у), подобрать к точкам (xi , yi ) график функции (от руки, с помощью линейки или лекала) и найти ординату у для интересующего нас х. Если значение х находится в пределах интервала изменения [x1 , xN], то подобная процедура называется интерполяцией. Если оно находится за пределами этого интервала – то экстраполяцией.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.