Коллоидная химия: Лабораторный практикум, страница 32

Приложение 2

Графическая обработка результатов измерений

Пары чисел (х, у), находящихся во взаимном соответствии, могут быть представлены не только таблицей, но и графически в виде диаграммы в координатах х, у. Если числа (х, у) явля­ются результатами измерений и, следовательно, содержат ошибки измерений, их графическое изображение называется диаграммой рассеяния. Пары чисел в этом случае изображаются от­дельными "точками" на плоскости (х, у). Такие диаграммы являются типичными для математики дискретных переменных, например в математической статистике. Если числа (х, у) представляют функциональную зависимость у = ¦(х), в которой аргумент х является непрерывной переменной, а функция у может быть вычислена с произвольно высокой точностью для любого х в некотором диапазоне изменения х, диаграмма называется графиком функции у = ¦(х). Зависимость у = ¦(х) в этом случае изображается непрерывной линией, которую следует рассматривать как множество точек (х, у), сливающихся в одну линию. Такие диаграммы являются типичными для математики непрерывных переменных, например в математическом анализе.

В экспериментальных исследованиях часто используют комбинированные диаграммы, со­вмещающие диаграмму рассеяния и график функции в одних координатных осях (х, у). (В обиходе, такую комбинацию называют просто графиком). Это совмещение базируется на предположении, что функциональная зависимость, график которой изображен, лежит в основе соответствия между измеренными значениями х и у, и что экспериментальные точки принадле­жали бы данному графику функции, если бы не содержали погрешностей измерения.

2.1 Построение и обработка линейного графика

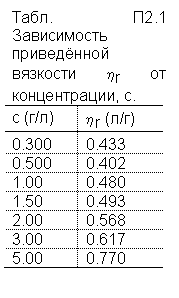
Рассмотрим построение и обработку линейного графика на частном примере. Пусть даны экспериментальные значения концентраций "с" растворов некоторого полимера и соответствующие им значения приведённой вязкости, как показано в таблице П2.1, причём для приведённой вязкости (см. лаб. работу 2) будем использовать сокращённое обозначение hr .

Из теоретических соображений и предшествующих исследований известно, что приведённая вязкость и концентрация связаны линейной функциональной зависимостью общего вида у = а + b×х, где  у = hr и х = с. В такого рода зависимостях параметр "а" называется свободным членом или начальной ординатой графика, а параметр b - угловым коэффициентом или коэффициентом наклона. Задача графической обработки – найти параметры а и b, которые наилучшим образом удовлетворяют данным в таблице П2.1.

Построение любого графика полезно разбить на отдельные стадии.

1) Решить, какие числа отвечают независимой переменной х и какие  – функции у, и записать имеющиеся пары чисел в виде таблицы в порядке увеличения независимой переменной. В данном примере эта стадия уже пройдена (табл. П2.1).

2) Выбрать приблизительный размер графика соответственно целям и сложности графического построения. Если график нужен для целей иллюстрации, то есть чтобы видеть "ход" изменения "у" при изменении "х", можно выбрать небольшой размер, например четверть или даже меньшую часть обычного листа. Если он нужен для дальнейшей графической обработки (дополнительных построений и измерений), размер должен быть настолько большим, чтобы точность измерений на нём была не меньше точности измерения физических величин, для которых он строится. Для линейных графиков обычно бывает достаточно половины или одной трети формата А4 (21 см × 29.7 см). В данном случае, можно выбрать приблизительный размер 10 см × 10 см, и на следующей стадии откорректировать его в большую или меньшую сторону.