Химия \ Коллоидная химия

Коллоидная химия: Лабораторный практикум, страница 29

Для определения кинетических параметров предельной степени набухания aMAX и константы набухания kН, постоянных для данного полимера приведем уравнение (8.2) к виду

             (8.3)

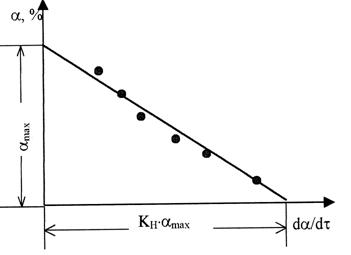
Построить график, по оси абсцисс отложить значения da/dt, по оси ординат - a.

Подпись: Рис. 8.2 Определение скорости набухания по кинетической кривой. Уравнение (8.3) представляет собой уравнение прямой, которая отсекает на оси ординат отрезок равный aMAX, а на оси абсцисс – отрезок равный aMAX× kН (см. рис. 8.3).

Контрольные вопросы

1.  Подпись: Рис. 8.3 Определение кинетических параметров процесса набухания. Набухание ВМС, степень набухания

2.  Ограниченное и неограниченное набухание

3.  Назовите факторы, влияющие на характер набухания ВМС

4.  Стадии процесса набухания

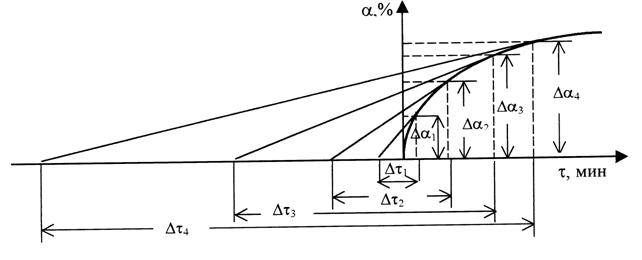
5.  Опишите зависимость скорости ограниченного набухания от времени (см. рис. 8.2)

6.  Перечислите факторы, влияющие на кинетику процесса


Литература

Балакирев А.А., Бабак В.Г., Дехтяренко Н.Г., Иванова И.А., Монисова Р.А. Коллоидная химия. Лабораторный практикум. Часть 2. М: ВЗИПП 1986, Лаб. работа 11.

Зимон А.Д., Лещенко Н.Ф. Коллоидная химия. М: Химия, 1995, Глава 19.

Воюцкий С.С. Курс коллоидной химии. М: Химия, 1975, Глава 14.

Приложение 1

Правила представления результатов измерений и вычислений

Результаты измерений и вычислений выражаются числами. Обычная проблема, с которой сталкиваются студенты – сколько цифр должно быть указано в числе и где следует поместить разделительную запятую или точку. В отношении этого в точных науках существуют общеприня­тые правила, которым необходимо следовать. Эти правила основываются на том, что любые из­мерения имеют естественные погрешности, и эти погрешности распространяются на результаты вычислений, когда результаты измерений используются в математических формулах.

Одно из самых простых правил, которое следует иметь в виду, когда мы имеем дело с числами, касается количества значащих цифр в числе. Значащими цифрами называют все запи­санные цифры числа, за исключением нулей, показывающих положение первой ненулевой цифры после разделительной запятой. Например, число 14 см записано с двумя значащими циф­рами, число 140 мм – с тремя, число 1.4×102 мм – с двумя, число 1.40×102 мм – с тремя, число 0.14 м – с двумя, число 0.00014 км – с двумя, число 1.400×10–4 км – с четырьмя.

Упомянутое выше правило формулируется так. Число значащих цифр в записи числа должно быть равно числу достоверных цифр плюс одна недостоверная. Ка­кие цифры являются достоверными и какие нет зависит от происхождения числа. Наиболее про­сто этот вопрос решается, когда число является непосредственным результатом измерения или результатом округления. Пусть, например, мы измеряем длину прямоугольного куска ткани с по­мощью швейного "сантиметра" или рулетки с ценой деления 1 мм. Если один обрез куска поме­щён у нуля, а другой оказался между 140 мм и 141 мм, но ближе к 140 мм, мы должны запи­сать 140 мм. Здесь цифры 1 и 4 являются достоверными, а цифра 0 – недостоверной, причём её недостоверность составляет 1 мм в соответствии с ценой деления измерительного инструмента. Разумеется, при хорошем зрении можно оценить находится ли обрез ткани ближе к метке 140 мм или к середине между метками 140 и 141 мм, то есть к 140.5 мм. Однако следует иметь в виду, что существует дополнительная неопределённость, по крайней мере 0.5 мм, в расположении об­реза ткани около нуля инструмента. В экспериментальных науках принято, что недостоверность однократного (то есть проведённого один раз) измерения равна цене деления измерительного прибора, если в характеристиках прибора не указано иначе·.

Скачать файл