Коллоидная химия: Лабораторный практикум, страница 34

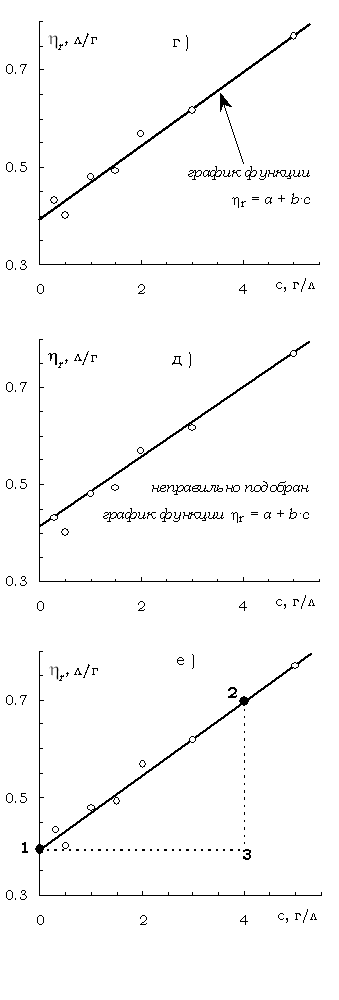
7) В заключении следует найти коэффициенты а и b построенного графика у = а + b×х. Для этого следует выбрать любые две точки, принадлежащие графику (например, точки 1 и 2 на рис. П2.1 е), определить их координаты (х₁,у₁) и (х₂,у₂) и вычислить

  ,  , или 

Процедура вычисления углового коэффициента эквивалентна нахождению тангенса угла наклона графика к оси абсцисс путём решения прямоугольного треугольника 1-2-3 (рис. П2.1 е). Действительно, разности у₂ – у₁ и х₂ – х₁ представляют длины катетов этого треугольника, взятые в единицах измерения физических величин, отложенных по соответствующим осям. К сожалению, формулировка "найти тангенс угла наклона графика" может провоцировать ошибочные действия. Если Ð(3-1-2) измерить транспортиром в градусах и затем вычислить тангенс этого угла, то, в общем случае, получится неправильный результат, потому что наблюдаемый угол зависит от масштабов, принятых для осей координат. В этом легко убедиться, если сравнить наклоны графиков на рис. П2.1 е и в, которые построены для одних и тех же чисел, но с разными масштабами по осям ординат.

2.2 Графическая обработка нелинейных зависимостей

Нелинейные функциональные зависимости между физическими величинами являются наименее благоприятными для их анализа графическими или вычислительными методами. Поэтому, если возможно, их преобразуют в линейные зависимости. Эта процедура называется линеаризацией. Например, рассмотренная выше зависимость приведённой вязкости от концентрации является продуктом линеаризации уравнения Хаггинса                         h = h_о(1 + а×с + b×с²)

где h - вязкость раствора полимера, h_о – вязкость раствора при концентрации с = 0 (то есть вязкость растворителя), а и b – коэффициенты, значения которых определялись в предыдущем разделе П2.1. Чтобы преобразовать эту зависимость в линейную делаются следующие выкладки:

= 1 + а×с + b×с² ;      – 1 = а×с + b×с² ;      = а×с + b×с² ;        = а + b×с

Последнее уравнение в этой серии является линейным, вида y = a + b×x, где х = с и у = hr = .

К сожалению, процедура линеаризации возможна далеко не всегда. Существует много зависимостей y = ¦(x), точный вид функции ¦ которых не известен и которые не могут быть линеаризованы по этой причине. Обычная задача, с которой приходится сталкиваться в этом случае, – нахождение производной (dy/dx) при некотором значении х графическим методом.

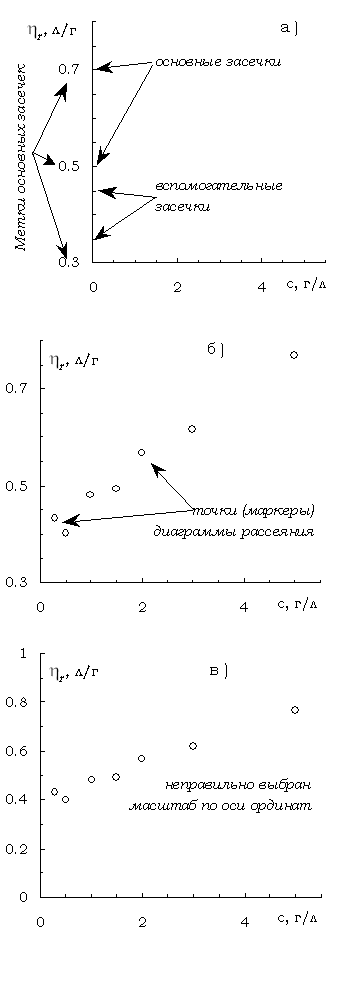
Для решения этой задачи следует выбрать по возможности большой размер графика (например целый лист формата А4) и использовать те же стадии построения, которые описаны в приложении 2.1. вплоть до стадии построения диаграммы рассеяния. На следующей стадии, построение графика "по точкам" осуществляется, в общем, по тому же принципу минимального отклонения точек от графика функции. Особенность этой стадии заключается в том, что она является менее определённой и допускающей больше произвола, чем в случае линейного графика. Всё же, как правило, эта стадия не является полностью произвольной, потому что мы обычно знаем кое-что о функции, с которой имеем дело. Мы можем знать, например, является она убывающей или возрастающей, имеет ли экстремум (максимум или минимум), асимптоту, точки перегиба (точки, в которых чередуется выпуклость и вогнутость кривой), или какие-то частные точки (например, значение у при х = 0). Такие знания необходимо использовать для сокращения неопределённости и произвольности в построении графика.