Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 8

Гіпотеза (5.7) є узагальненням на випадок декількох факторів аналогічного припущення про сталість фактора X у випадку лінійної двухфакторной моделі.

Тим самим виявляється, що у вектора єдиним джерелом збурювань є випадковий вектор . У цьому випадку говорять, що властивості шуканих оцінок і критеріїв обумовлені матрицею спостережень X.

Гіпотеза (5.8) характеризує, по-перше, відсутність строгої лінійної залежності між пояснюючими перемінними  і, по-друге, що число спостережень n більше числа пояснюючих перемінних k. У співвідношенні (5.8) позначення виражає ранг матриці X.

Приналежність вектора збурювань  безлічі нормально розподілених векторних випадкових величин, виражена в (5.9), фактично поєднує припущення (5.5) і (5.6).

5.2. Перебування оцінки  вектора  методом найменших квадратів

Позначимо через  - вектор-стовпець, що оцінює вектор . Можемо записати:

                                       (5.10)

де через  позначений вектор-стовпець залишків  .

Критерій - сума квадратів компонент вектора залишків - має вид

 .                  (5.11)

Для перебування значення , минимизирующего цю суму квадратів відхилень, продифференцируем (5.11) по . Дорівнюючи отримане вираження нульовому вектору, одержуємо систему нормальних рівнянь у векторно-матричной формі (порівняй з (3.14)):

 .                                          (5.12)

На основі гіпотези (5.8) одержуємо основний результат:

 .                                      (5.13)

Оцінка  вектора параметрів  знайдена.

5.3. Властивості оцінок вектора параметрів  

Підставляючи (5.3) у (5.13), можна одержати наступне важливе представлення для оцінки :

 .                                (5.14)

Звідси відразу випливає, що

 .                                          (5.15)

Результат (5.15) означає, що вектор оцінок   є незміщеним.

Можна показати, що ковариационная матриця вектора оцінок  має вид:

 .               (5.16)

Рівність (5.16) означає, що дисперсія компонента  вектора  може бути оцінена шляхом перемножування i-го елемента головної діагоналі матриці  на дисперсію випадкового збурювання . Аналогічно ковариация пари оцінок  і  визначається множенням (i,j)-го елемента матриці  на .

Підсумовуючи розгляд властивостей оцінок  , відзначимо, що в силу припущення (5.9) вектор  має багатомірний нормальний розподіл, тобто

.                                   (5.17)

5.4. Гіпотези про значимість оцінок типу

Якщо дисперсія  збурювань U відома, то факти, представлені співвідношеннями  (5.13), (5.14), (5.16) можуть бути безпосередньо використані для перевірки значимості компонент вектора  і побудови довірчих інтервалів. У випадку незнання  можна надійти в такий спосіб. Тому що  і  є лінійні комбінації нормально розподілених випадкових величин, то вони теж розподілені нормально. Можна показати, що , де  – нульова матриця з n рядків і k стовпців. Останнє означає, що вони розподілені незалежно друг від друга.

Цей результат дозволяє використовувати t-розподіл для перевірки гіпотез щодо кожного з регресійних коефіцієнтів . Величина має незалежне від  розподіл з ( ) ступенями волі. Звідси по визначенню t-розподілу величина

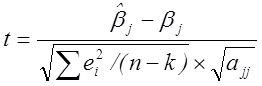                               (5.18)

задовольняє t-розподілу зі ступенями волі.

Гіпотеза про значимість  перевіряється в такий спосіб. У (5.18) підставляємо цікавляче нас гіпотетичне значення  і розраховуємо t. Значення t порівнюємо з критичним , відповідним ступеням волі і  %-му рівню довіри. Якщо виявиться, що виконано нерівність

 ,

те гіпотеза про значимість  відкидається.

Прикладом перевірки відсутності лінійної залежності Y від  є перевірка гіпотези H₀ : .

Співвідношення (5.18) дає  %-ный довірчий інтервал для  виду

Розглянемо підхід до спільної перевірки гіпотез щодо декількох чи усіх .

Висунемо нульову гіпотезу

                                           (5.19)

проти альтернативної , що складається в тім, що не усі  дорівнюють нулю. Вектор . Нульова гіпотеза припускає, що отсутствует вплив усіх  факторів  на .

Можна показати, що для перевірки нульової гіпотези (5.19) застосуємо F-критерій виду

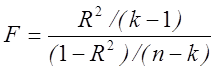 ,                                    (5.20)

де – коефіцієнт детермінації (квадрат коефіцієнта множинної кореляції).

Гіпотеза  (5.19) при 100 %-ном рівні значимості відхиляється, якщо виконана нерівність

 ,                                          (5.21)

де F розраховується по формулі (5.20), а визначається з таблиці теоретичних значень F-критерію при 100 %-ном рівні значимості і (k-1), (n-k) ступенях волі. Це значення можна визначити за допомогою функції EXCEL FРАСПОБР( , k-1, n-k) Відхилення гіпотези  змістовно означає, що між фактором Y і усіма факторами  мається лінійний статистичний зв'язок. Про силу зв'язку можна судити по величині коефіцієнта детермінації .

Використовуючи результати сьогодення роздягнула, можна ставити і вирішувати задачі чи додавання виключення одного і/чи декількох факторів . Докладніше про це див. у [4, стор. 144-147].

5.5. Прогноз

Подальше використання співвідношень типу (5.1) зв'язано з одержанням інформації про очікуване значення фактора Y, що повинне відповідати деякому сполученню значень факторів , що не наблюдались у вибірці. Якщо ототожнити номера спостережень 1,2,…,nс номерами тимчасових періодів, то конкретизація задачі прогнозування може виглядати так: по очікуваним у періоді n+1 значенням вектора

потрібно побудувати прогноз очікуваного значення , тобто M(Y_n+1| ). З урахуванням співвідношення (5.2) одержимо

Можна побудувати або крапковий, або интервальный прогноз.

Найкращий лінійний незміщений прогноз для  має вид . Тому шуканий крапковий прогноз є

 .                   (5.22)

Відповідний 100 %-ный довірчий інтервал для крапкового прогнозу має вид

 .   (5.23)

У нерівностях (5.23) .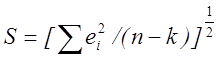

Таким чином, очікуване значення M(Y_n+1|C) величини Y_n+1 з імовірністю (1- ) накривається інтервалом (5.23).

Задача интервального прогнозування складається в побудові довірчого інтервалу не для середнього M(Y_n+1|C), а для ізольованого значення Y_n+1, що повинне асоціюватися з вектором .