Залучимо модель лінійної множинної регресії (5.26). Для економії зусиль ширше використовуємо можливості електронної таблиці EXCEL і, зокрема, функцію ЛИНЕЙН(). Коротка довідка по застосуванню функції ЛИНЕЙН() приведена в додатку П2 (див. стор. 44).
Спочатку сформуємо вектор ![]() стосовно
до розширеної матриці екзогенних перемінні
стосовно
до розширеної матриці екзогенних перемінні ![]() моделі
(5.26). Розширена матриця має вид
моделі
(5.26). Розширена матриця має вид
|
1 |
15185 |
101,5 |
3,81 |
1 |
|
|
1 |
15366 |
101,0 |
3,39 |
2 |
|
|
1 |
15937 |
101,0 |
4,04 |
3 |
|
|
1 |
16680 |
102,3 |
4,06 |
4 |
|
|
1 |
17496 |
102,4 |
4,03 |
5 |
|
|
1 |
18579 |
100,1 |
3,98 |
6 |
|
|
1 |
18816 |
99,0 |
4,02 |
7 |
|
|
1 |
19694 |
101,0 |
4,08 |
8 |
|
|
1 |
20468 |
101,4 |
4,12 |
9 |
|
|
1 |
20899 |
101,1 |
4,14 |
10 |
|
|
X = |
1 |
21042 |
102,9 |
4,20 |
11 |
|
1 |
22079 |
104,1 |
4,30 |
12 |
|
|
1 |
22052 |
104,6 |
4,30 |
13 |
|
|
1 |
22975 |
103,3 |
4,45 |
14 |
|
|
1 |
23632 |
102,0 |
4,50 |
15 |
|
|
1 |
25086 |
101,7 |
4,50 |
16 |
|
|
1 |
26031 |
102,1 |
4,39 |
17 |
|
|
1 |
27098 |
103,7 |
4,29 |
18 |
|
|
1 |
28127 |
99,9 |
4,24 |
19 |
|
|
1 |
29273 |
100,0 |
4,24 |
20 |
|
|
1 |
14822 |
102,6 |
4,22 |
21 |
|
|
1 |
28750 |
101,4 |
4,20 |
22 |
До другого, третього і четвертого стовпців матриці застосуємо функцію EXCEL ПРЕДСКАЗ(). У результаті шуканий вектор прийме вид
![]() .
.
Тепер для одержання оцінок параметрів рівняння множинної лінійної регресії (5.25) скористаємося функцією EXCEL ЛИНЕЙН(). У результаті одержимо підсумкову таблицю (див. табл. 5.2).
Звідси результуюче рівняння лінійної множинної регресії приймає вид
![]() .
.
Таблиця 5.2
Розрахункові оцінки функції ЛИНЕЙН()
|
508,189 |
-566,788 |
-618,346 |
-0,20664 |
75885,24 |
|
68,529 |
1606,14 |
199,2031 |
0,092151 |
18824,44 |
|
0,858 |
1134,491 |
|||
|
25,754 |
17 |
|||
|
132588202 |
21880205 |
Для
перевірки гіпотез про значимість оцінок регресійних параметрів визначаємо
теоретичне значення t-критерію: ![]()
![]() . Розподілом значень першого рядка
табл. 5.2 на другу одержуємо емпіричні значення t-статистики:
. Розподілом значень першого рядка
табл. 5.2 на другу одержуємо емпіричні значення t-статистики:
|
7,41 |
-0,353 |
-3,104 |
-2,242 |
4,031 |
Порівнюємо їх з теоретичним і одержуємо, що нерівність
![]()
виконано для оцінок
![]() . Це означає незначимість впливу
грошового фактора і фактора безробіття на ВВП з імовірністю, не меншої 95 %.
Інші фактори виявляються значимими. Перевірка адекватності моделі в цілому
показує, що модель можна вважати адекватної (нерівність
. Це означає незначимість впливу
грошового фактора і фактора безробіття на ВВП з імовірністю, не меншої 95 %.
Інші фактори виявляються значимими. Перевірка адекватності моделі в цілому
показує, що модель можна вважати адекватної (нерівність
25,754=![]() = FРАСПОБР(0,05;5;17)=2,81
= FРАСПОБР(0,05;5;17)=2,81
виконано).
Виконаємо
підстановку значень вектора ![]() в рівняння й
одержимо прогнозну оцінку
в рівняння й
одержимо прогнозну оцінку
![]() ,
,
що практично збігається з прогнозною оцінкою у випадку обліку залежності ВВП тільки від фактора часу t.
Отриманий результат можна проінтерпретувати як факт неповноти набору використаних факторів і даних. Висновок полягає в тому, що для побудови задовільного крапкового прогнозу ВВП по наявних факторних ознаках, що характеризує стан макроекономіки України, виявляється достатнім використовувати фактор часу.
– гіпотезу лінійності
![]() ;
;
–
припущення про те, що випадкові перемінні Ui мають нульове математичне чекання ![]() ;
;
–
властивість некоррелированности випадкових величин ![]() ;
;
–
властивість гомоскедастичности випадкових величин ![]() ;
;
–
припущення про фіксованість матриці
![]() ;
;
–
матриця ![]() має повний ранг,
рівний
має повний ранг,
рівний ![]() ;
;
–
вектор збурювань ![]() належить безлічі нормально розподілених
векторних випадкових величин.
належить безлічі нормально розподілених
векторних випадкових величин.
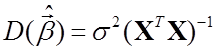 .
.
![]() .
.
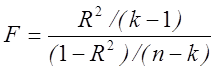 .
.
![]() .
.
 .
.
1. У чому складається основна задача дослідження загальної лінійної регресійної моделі?
2. Що таке – матриця регрессоров?
3. Охарактеризувати властивість гомоскедастичности.
4. Одержати оцінку
![]() вектора параметрів
вектора параметрів ![]() .
.
5.
Якими властивостями володіє оцінка ![]() вектора
параметрів
вектора
параметрів ![]() ?
?
6.
Сформулювати гіпотезу про значимість ![]() .
.
7. Як перевірити гіпотезу про адекватність лінійної моделі?
8. Сформулювати задачу крапкового прогнозування.
9. Сформулювати задачу интервального прогнозування.
Використовуючи результати рішення свого варіанта завдання з п.3 (табл. П1 на стор. 43), побудувати крапковий прогноз на курсу валют на восьмий день.
|
Регрессор Некореллированность Багатомірний нормальний закон розподілу Крапковий прогноз |
Лінійність Гомоскедастичность Обумовленість Интервальный прогноз |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.