Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 5

  суму квадратів, що характеризує, відхилень вихідних вимірів ознаки Y від крапок прямої (3.12), розрахованих для значень X_i.

Принцип найменших квадратів складається у виборі таких  і , для яких величина (3.13) буде мінімальною.

Для перебування  і  використовують необхідні умови экстремума у виді

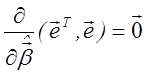 ,                                      (3.14)

де

Співвідношення (3.14) являє собою систему рівнянь, що в остаточному виді записується як

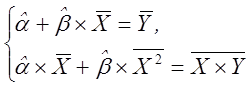                             (3.15)

і називається системою нормальних рівнянь. Тут

 .

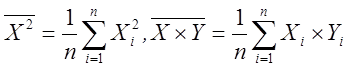З першого рівняння випливає, що оцінки  і  методу найменших квадратів задовольняють рівнянню прямої, що проходить через крапку з координатами ( ).

Рішення системи нормальних рівнянь (3.15) має вид:

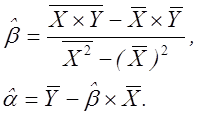                                  (3.16)

Оцінки  і  мають наступні властивості.

Властивість 1. Оцінки  і  є лінійними комбінаціями спостережень Y_i.

Визначення. Оцінка  параметра  називається незміщеної, якщо виконана умова .

Властивість 2. Величини  і  є незміщеними оцінками параметрів  і .

Можна показати, що дисперсії оцінок і  мають вид:

 ,                       (3.17)

а їх ковариация –

 ,                             (3.18)

де .

Визначення. Оцінка  параметра  називається найкращої, якщо в класі всіх лінійних незміщених операторів оцінювання виду , де , величина , а  – довільна константа, вона має найменшу дисперсію.

Властивість 3. Оцінки і  є найкращими.

Можна показати, що незміщена оцінка  невідомої дисперсії  може бути узята у виді

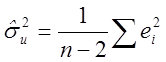.                                      (3.19)

3.3. Приклад

Потрібно побудувати эконометрическую модель залежності витрат на одиницю продукції від рівня її фондоемкости. Вихідні дані в умовних одиницях представлені в другому і третьому стовпцях таблиці 3.1.

Рішення.

Нехай залежність між витратами на одиницю продукції і рівнем фондоемкости характеризується рівнянням прямої Y = α + β×X + u, де Y – витрати на одиницю продукції; X – рівень фондоемкости; u – залишки.

Розрахункові значення витрат на одиницю продукції (величини ) можна знайти, скориставшись моделлю

 .

Оцінки параметрів  і  знаходимо, вирішуючи систему нормальних рівнянь (3.15):

 .

Таблиця 3.1

Вихідні дані і проміжні розрахунки для приклада

№ п/п
1	50	90	8100	4500	-10,8	-4,2	116,64	45,36
2	40	75	5625	3000	-25,8	-14,2	665,64	366,36
3	65	120	14400	7800	19,2	10,8	368,64	207,36
4	55	100	10000	5500	-0,8	0,8	0,64	-0,64
5	45	80	6400	3600	-20,8	-9,2	432,64	191,36
6	42	78	6084	3276	-22,8	-12,2	519,84	278,16
7	56	110	12100	6160	9,2	1,8	84,64	16,56
8	60	115	13225	6900	14,2	5,8	201,64	82,36
9	64	115	13225	7360	14,2	9,8	201,64	139,16
10	65	125	15625	8125	24,2	10,8	585,64	261,36
Сума	542	1008	104784	56221			3177,6	1587,40
Середнє	54,2	100,8	10478,4	5622,1			317,76	158,74

Продовження таблиці 3.1

48,80	1,20	1,43	17,64
41,31	-1,31	1,72	201,64
63,79	1,21	1,46	116,64
53,80	1,20	1,44	0,64
43,81	1,19	1,42	84,64
42,81	-0,81	0,66	148,84
58,80	-2,80	7,82	3,24
61,29	-1,29	1,67	33,64
61,29	2,71	7,32	96,04
66,29	-1,29	1,66	116,64
Сума		26,60	819,60
Середнє		2,66	81,96

Її рішення має вид . Эконометрическая модель виглядає в такий спосіб

 .

Отриманий результат допускає наступне тлумачення. Тому що вільний член моделі (3,8)  не дорівнює нулю, то рівень витрат на одиницю продукції не строго пропорційний рівню фондоемкости. Величина 0,5 показує, що при збільшенні фондоемкости продукції на одну умовну одиницю витрати на единицу продукції зростають на 0,5.

3.4. Питання до теми 3

1. Які припущення щодо зв'язку виду X → Y  необхідні?
2. Розкрити сутність методу найменших квадратів.
3. Назвати приклади функціональних залежностей між перемінними X і Y.
4. Указати мета дослідження залежності між факторами Y і Y.
5. Назвати причини введення в рівняння регресії фактора випадковості.
6. Що таке система нормальних рівнянь?
7. Якими властивостями володіють оцінки і ?
8. Як інтерпретуються параметри рівняння лінійної регресії?

3.5. Задачі для самостійного рішення

Задано динаміку курсу валюти за сімох місяців (дані умовні). Потрібно побудувати лінійну регресійну модель зміни курсу валюти в залежності від часу і дати інтерпретацію отриманому результату. Вихідні дані представлені в табл. П.1 (див. стор. 43).

3.6. Основні терміни і поняття

Ідентифікація Специфікація форми зв'язку  Фактор стохастичности

Рівняння лінійної регресії Система нормальних рівнянь Несмещенность

Тема 4. Дослідження найпростішої эконометрической моделі