Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 14

У цьому розділі ми розглянемо окремий випадок узагальненої регресійної моделі, а саме, модель з гетероскедастичностью. Це означає, що помилки некоррелированы, але мають непостійні дисперсії. (Класична модель з постійними дисперсіями помилок називається гомоскедастичной.) Як уже відзначалося, гетероскедастичность досить часто виникає, якщо аналізовані об'єкти, говорячи нестрого, неоднорідні. Наприклад, якщо досліджується залежність прибутку підприємства від яких-небудь факторів, скажемо, від розміру основних фондів, те природно очікувати, що для великих підприємств коливання прибутку буде вище, ніж для малих.

Метод зважених найменших квадратів

Отже, нехай

                                              (6.6)

і припустимо, що ковариационная матриця  вектора помилок диагональна, , t = l, ..., n. Іноді зручно використовувати представлення , де числа , нормовані таким чином, що . Тоді при = 1, t = 1, ..., n, модель зводиться до класичного.

Узагальнений метод найменших квадратів у даному випадку виглядає дуже просто — допоміжна система виходить розподілом кожного рівняння в (6.6) на відповідне , (тут нам зручніше виписати кожне рівняння):

 ,                               (6.7)

де  причому , при . Застосовуючи до (6.7) стандартний метод найменших квадратів, ОМНК-оценку одержуємо мінімізацією по  суми

 .

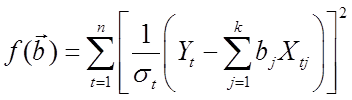Неважко зрозуміти змістовний зміст цього перетворення. Використовуючи звичайний метод найменших квадратів, ми мінімізуємо сумуквадратів відхилень 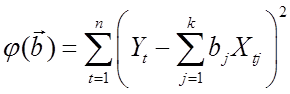 у який, говорячи нестрого, різні доданки дають різний статистичний внесок через різні дисперсії, що в остаточному підсумку і приводить до неефективності МНК-оценки. "Зважуючи" кожне спостереження за допомогою коефіцієнта , ми усуваємо таку неоднорідність. Тому часто узагальнений метод найменших квадратів для системи з гетероскедастичностью називають методом зважених найменших квадратів. Можна безпосередньо перевірити, що застосування методу зважених найменших квадратів приводить до зменшення дисперсій оцінок у порівнянні а звичайному методі найменших квадратів.

Корекція на гетероскедастичность

Якщо числа , невідомі (що, як правило, і буває на практиці), необхідно використовувати доступний узагальнений метод найменших квадратів, що вимагає оцінювання дисперсій . Тому що число цих параметрів дорівнює п, те без додаткових обмежень на структуру матриці  немає надії одержати прийнятні оцінки дисперсій. Нижче ми розглянемо один клас моделей з гетероскедастичностью, де такі обмеження накладаються і завдяки цьому вдається побудувати задовільні оцінки матриці , а отже, використовуючи доступний узагальнений метод найменших квадратів, і оцінку .

Помилка пропорційна незалежної перемінний. У деяких ситуаціях апріорно можна вважати, що помилка прямо пропорційна однієї з незалежних перемінних, наприклад, : . Тоді, розділивши t-e. рівняння на , t=1, ..., n, і вводячи нові незалежні перемінні  і нову залежну перемінну , t=1,...,n, j=1,...,k, одержимо класичну регресійну модель. МНК-оценки коефіцієнтів цієї моделі дають безпосередньо оцінки вихідної моделі. Варто тільки пам'ятати, що якщо перший регрессор у Х є набір одиниць, то оцінки вільного члена і коефіцієнта при  в новій моделі є оцінками відповідно коефіцієнта при  і вільному члені у вихідній моделі.

Виникає природне запитанння, при яких обставинах можна користатися описаним вище методом. Існують процедури, що дозволяють виявляти гетероскедастичность того чи іншого роду (тести на гетероскедастичность) [4-6]. Тут ми обмежимося лише практичними рекомендаціями. Якщо є припущення про залежність помилок від однієї з незалежних перемінних, то доцільно розташувати спостереження в порядку зростання значень цієї перемінний, а потім провести звичайну регресію й одержати залишки. Якщо розмах їхніх коливань теж зростає (це добре помітно при звичайному візуальному дослідженні), то це промовляє на користь вихідного припущення. Тоді треба зробити описане вище перетворення; знову провести регресію і досліджувати залишки. Якщо тепер їхнє коливання має неупорядкований характер, то це може служити показником того, що корекція на гетероскедастичность пройшла успішно. Природно, варто порівнювати й інші параметри регресії (значимість оцінок, суму квадратів відхилень і т.п.) і тільки тоді приймати остаточне рішення, яка з моделей більш прийнятна.

6.5.2. Кореляція за часом

Авторегрессионный процес першого порядку

При аналізі тимчасових рядів часто приходиться враховувати статистичну залежність спостережень у різні моменти часу. Іншими словами, для багатьох тимчасових рядів припущення про некоррелированности помилок не виконується. У цьому розділі ми розглянемо найбільш просту модель, у якій помилки утворять так називаний авторегрессионый процес першого порядку (точне визначення буде дано нижче). Як було показано раніше (п. 6.3), застосування звичайного методу найменших квадратів до цієї системи дає незміщені і заможні оцінки параметрів, однак можна показати, що оцінка дисперсії виявляється зміщеної вниз, що може негативно позначитися при перевірці гіпотез про значимість коефіцієнтів. Образно говорячи, МНК малює більш оптимістичну картину регресії, чим є насправді.

Як і раніш, розглянемо модель

 ,                                              (6.8)

де t-я компонента вектора  представляє значення залежної перемінної в момент часу t, t = 1,...,n, а  – вектор випадкових помилок. Для зручності запишемо докладніше рівняння для спостереження в момент часу t:

                           (6.9)