Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 15

Один з найбільш простих способів обліку коррелированности помилок (у різні моменти часу) складається в припущенні, що випадкова послідовність  утворить авторегрессионый процес першого порядку. Цеозначає, що помилки задовольняють рекуррентному співвідношенню

                                             (6.10)

де  — послідовність незалежних нормально розподілених випадкових величин з нульовим середньої і постійною дисперсією , а  — деякий параметр, називаний коефіцієнтом авторегрессии ( ). Строго говорячи, для повного опису моделі треба визначити . Будемо вважати, що  — нормальна випадкова величина з нульовою середнім і дисперсією , що не залежить від {v_t, t = 1,...,n}. З подальшого стане ясно, чому в  саме такі параметри. Узявши математичне чекання від обох частин (6.10), одержимо , відкіля випливає, що . Оскільки виражається через  (див. (6.9)), те , і v_t, незалежні. Тому

 .

Легко перевіряється, що якщо , те

Множачи (6.10) на , і знову користаючись незалежністю , і v_t, одержимо

                  (6.11)

Аналогічно , і взагалі

 .                                     (6.12)

Таким чином, послідовність  утворить стаціонарний випадковий процес. Саме цією обставиною диктувався вибір параметрів початкової величини . Насправді, з часом залежність , від  швидко зменшується, тому в більшості книг по эконометрике проблему початкових умов для  просто не розглядають, неявно припускаючи, що процес (6.10) при будь-якім початковому значенні швидко сходиться до стаціонарного. Відзначимо також, що умова  є необхідним для стаціонарності.

З (6.11) випливає, що

 ,

тобто  є в точності коефіцієнт кореляції між двома сусідніми помилками. Користаючись (6.12), можна виписати ковариационную матрицю випадкового вектора :

 .

Оцінювання в моделі з авторегрессией

Проблему оцінювання системи (6.8) розглянемо окремо для випадку, коли коефіцієнт  відомий, і окремо — коли невідомий.

1. Значення  відоме. У цьому випадку для оцінювання системи (6.5) можна застосувати узагальнений метод найменших квадратів. У даному випадку неважко знайти матрицю Р, для якої P^TP = . Тут дуже просто догадатися, яке лінійне перетворення вихідної системи (6.8) треба провести, щоб одержати класичну модель. Випишемо (6.9) для моменту часу t – 1 (t > 0)

 ,

помножимо обох частин на  і віднімемо почленно з (6.9). Тоді з обліком (6.10) одержимо

 . (6.13)

При t = 1 досить обидві частини рівняння (6.9) помножити на :

 (6.14)

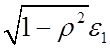У системі (6.13), (6.14) помилки задовольняють умовам уже звичайної регресійної моделі. Дійсно, у (6.13) випадкові величини { , t=2,...,n} незалежні і мають постійну дисперсію , а в (6.14) помилка  не залежить від { , t=2,...,n} і, згідно (6.11), також має дисперсію .

На практиці часто опускають перетворення (6.14), ігноруючи тим найперше спостереження. З одного боку, завдяки цьому, перетворення вихідної моделі (6.8) стає однаковим. Зокрема, для одержання оцінки параметра  досить оцінку вільного члена в (6.13) розділити на . З іншого боку, відкидання першого спостереження може привести до утрати важливої інформації, особливо у вибірках невеликого розміру.

2. Значення  невідоме. Ситуації, коли параметр авторегрессии  відомий, зустрічаються вкрай рідко. Тому виникає необхідність у процедурах оцінювання при невідомому . Як правило, вони мають ітеративний характер. Опишемо одну з найбільш уживаних. Ми не будемо встановлювати збіжність цих процедур. Практика їхнього застосування показала, що вони досить ефективні.

ПроцедураКохрейна-Оркатта (Cochrane-Orcutt). Початковим кроком цієї процедури є застосування звичайного методу найменших квадратів до вихідної системи (6.8) і одержання відповідних залишків . Далі,

1) як наближене значення  беретьсяйого МНК-оценка  в регресії ;

2) проводиться перетворення (6.13) (чи (6.13), (6.14))при  і знаходяться МНК-оценки  вектора параметрів ;

3) будується новий вектор залишків ;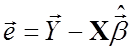

4) процедура повторюється, починаючи з п. 1.

Процес звичайно закінчується, коли чергове наближення мале відрізняється від попереднього. Іноді просто фіксується кількість ітерацій. Процедура Кохрейна-Оркатта реалізована в більшості эконометрических комп'ютерних програм. При її використанні може случитися, що значення параметра  буде знайдено неточно. Це зв'язано з тим, що при його оцінюванні може бути фактично знайдений локальний, а не глобальний мінімум квадратів відхилень у регресії п. 1.

6.6. Короткі висновки

1. Регресійні моделі є гнучким інструментом, що дозволяє оцінювати вплив якісних ознак на досліджувану перемінну.

2. У випадку  повної коллинеарности не можна побудувати MHK-оцінку вектора параметрів .

3. Найбільш характерні ознаки мультиколлинеарности наступні:

3.1. Невелика зміна вихідних даних приводить до істотної зміни оцінок коефіцієнтів моделі.

3.2. Оцінки мають великі стандартні помилки, малу значимість, у той час як модель у цілому є значимої.

3.3. Оцінки коефіцієнтів мають неправильні з погляду теорії чи знаки невиправдано великі значення.

4. За допомогою фіктивних перемінних можна досліджувати вплив різних якісних ознак (наприклад, рівень утворення і чи наявність відсутність дітей), а також їхній взаємний вплив.

5. Для дослідження впливу якісних ознак у модель можна вводити бінарні (фіктивні) перемінні, котрі, як правило, приймають значення 1, якщо дана якісна ознака присутній у спостереженні, і значення 0 при його відсутності.

6. Спосіб включення фіктивних перемінних залежить від апріорної інформації щодо впливу відповідних якісних ознак на залежну перемінну і від гіпотез, що перевіряються за допомогою моделі.