Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 12

Якщо якісна ознака, що включається в розгляд, має не два, а кілька значень, то в принципі можна було б увести дискретна перемінна, приймаюча така ж кількість значень. Але цього фактично ніколи не роблять, тому що тоді важко дати змістовну інтерпретацію відповідному коефіцієнту. У цих випадках доцільніше використовувати трохи бінарних перемінних. Типовим прикладом подібної ситуації є дослідження сезонних коливань. Нехай, наприклад, у_t — обсяг споживання деякого продукту на місяць t, і є всі підстави вважати, що споживання залежить від часу року. Для виявлення впливу сезонності можна ввести три бінарні перемінні d₁, d₂, d₃:

d_i1 = 1, якщо місяць t є зимовим, d_i1 = 0 в інших випадках;

d_i2. = 1, якщо місяць / є весняним, d_i2 = 0 в інших випадках;

d_i3 = 1, якщо місяць / є літнім, d_i3 = 0 в інших випадках, і оцінювати рівняння

                   (6.1)

Відзначимо, що ми не вводимо четверту бінарну перемінну d₄, що відноситься до осені, інакше тоді для будь-якого місяця t виконувалася б тотожність d_i1 + d_i2 + d_i3 + d_i4 = 1, що означало б лінійну залежність регрессоров у (6.1) і, як наслідок, неможливість одержання МНК-оценок.

Фіктивні перемінні, незважаючи на свою зовнішню простоту, є дуже гнучким інструментом при дослідженні впливу якісних ознак.

На закінчення цього розділу відзначимо, що за допомогою фіктивних перемінних можна досліджувати вплив різних якісних ознак (наприклад, рівень утворення і чи наявність відсутність дітей), а також їхній взаємний вплив. Варто тільки бути уважним, щоб при включенні декількох бінарних перемінних не порушити лінійну незалежність регрессоров (див. вище приклад із сезонними коливаннями).

6.3. Приватна кореляція

У тому випадку, коли мається однією незалежна й однією залежна перемінні, природною мірою залежності (у рамках лінійного підходу) є (вибірковий) коефіцієнт кореляції між ними. Використання багатомірної регресії дозволяє узагальнити це поняття на випадок, коли мається трохи незалежних перемінних. Коректування тут необхідне по наступним розуміннях. Високе значення коефіцієнта кореляції між досліджуваної залежною і який-небудь незалежною перемінною може означати високий ступінь залежності, але може бути обумовлено й іншою причиною. А саме, існує третя перемінна, котра впливає на дві перші, що і служить, у кінцевому рахунку, причиною їхній високий коррелированности. Тому виникає природна задача знайти "чисту" кореляцію між двома перемінними, виключивши (лінійне) вплив інших факторів. Це можна зробити за допомогою коефіцієнта приватної кореляції.

Для простоти припустимо, що мається звичайна двовимірна регресійна модель

де, як звичайно, — n×1 вектор спостережень залежної перемінний, ,  — n×1 вектори незалежних перемінних,  — (скалярні) параметри,  — n×1 вектор помилок. Наша мета — визначити кореляцію між  і, наприклад, першим регрессором  після виключення впливу .

Відповідна процедура улаштована в такий спосіб.

1. Здійснимо регресію  на  і константу й одержимо прогнозні значення .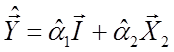

2. Здійснимо регресію  на  і константу й одержимо прогнозні значення .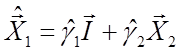

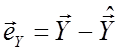3. Видалимо вплив , узявши залишки  і .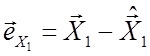

4. Визначимо (вибірковий) коефіцієнт приватної кореляції між  і  при виключенні впливу  як (вибірковий) коефіцієнт кореляції між  і :

                                   (6.2).

З властивостей методу найменших квадратів випливає, що  і  не коррелированы с. Саме в цьому змісті зазначена процедура відповідає інтуїтивному уявленню про «виключення (лінійного) впливу перемінної ».

Прямими обчисленнями можна показати, що справедливо наступна формулу, що зв'язує коефіцієнти приватної і звичайної кореляції:

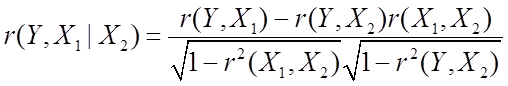 .                     (6.3)

Значення  лежать в інтервалі [-1,1], як у звичайного коефіцієнта кореляції. Рівність коефіцієнта  нулю означає, говорячи нестрого, відсутність прямого (лінійного) впливу перемінної  на .

Існує тісний зв'язок між коефіцієнтом приватної кореляції  і коефіцієнтом детермінації , а саме

 .

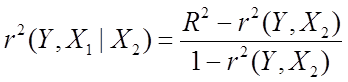Описана вище процедура очевидним образом узагальнюється на випадок, коли виключається вплив не однієї, а декількох перемінних: досить перемінну  замінити на набір перемінних , зберігаючи визначення (6.2). Формула (6.3), природно, ускладниться.

Процедура покрокового добору перемінних

Коефіцієнт приватної кореляції часто використовується при рішенні проблеми специфікації моделі (див. далі п. 6.4). Зупинимося на цьому аспекті більш докладно.

Іноді дослідник заздалегідь знає характер залежності досліджуваних величин, спираючи, наприклад, на економічну теорію, що предыдут результати, апріорні знання і т.п., і завдання полягає лише в оцінюванні невідомих параметрів. (Власне кажучи, у всіх наших попередніх міркуваннях ми неявно припускали, що мається саме така ситуація.) Класичний приклад — оцінювання параметрів виробничої функції Кобба-Дугласа , де  — сукупний випуск, ДО — капіталовкладення і L — трудозатраты. Логарифмуючи цю рівність, одержуємо лінійне відносно  рівняння, з якого, наприклад, за допомогою методу найменших квадратів можна одержати оцінки цих параметрів, перевіряти ті чи інші гіпотези і т.д.

Однак на практиці досить часто приходиться зіштовхуватися із ситуацією, коли мається велике число спостережень різних параметрів (незалежних перемінних), але немає апріорної моделі досліджуваного явища. Виникає природна проблема, які перемінні включити в регресійну схему. Теоретичні питання, зв'язані з цією проблемою, будуть викладені далі, у п. 4.4.

У комп'ютерні пакети включені різні евристичні процедури покрокового добору регрессоров. Основними покроковими процедурами є процедура послідовного приєднання, процедура приєднання-видалення і процедура послідовного видалення. Опишемо коротко одну з таких процедур, що використовує поняття коефіцієнта приватної кореляції.

Процедура приєднання-видалення

На першому кроці з вихідного набору пояснюючих перемінних вибирається (включається в число регрессоров) перемінна, що має найбільший по модулі коефіцієнт кореляції з залежної перемінний Y.