Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 6

4.1. Перевірка гіпотез про значимість параметрів эконометрической моделі

4.1.1. Попередні зауваження

Щоб коректно висунути і потім перевірити гіпотези типу  де  – задані величини, необхідно визначитися з тим, яким є розподіл випадкової величини U чи спільний розподіл сукупності випадкових величин U₁, U₂, …, U_n поряд з умовами (3.9)- (3.11). Доповнимо ці умови вимогою, що U₁, U₂, …, U_n є випадковими величинами, що мають спільний нормальний закон розподілу.

Як показано в [4] (стор. 33-34), у цьому випадку оцінки  параметрів і  регресійного рівняння (3.8) є нормально розподіленими випадковими величинами, характеристики яких (середні, дисперсії і ковариации) збігаються з аналогічними вираженнями для і . Це означає і те, що визначено двовимірний розподіл для векторної випадкової величини ( ). Єдині труднощі перед перевіркою гіпотез відносно і зв'язані з наявністю у вираженнях для і невідомої дисперсії  возмущающей складової U.

Подальший виклад спирається на наступний результат: статистика  має -розподіл з (n-2) ступенями волі, і ця статистика не залежить від і . У твердженні використане позначення  для вираження .

Буде також використовуватися закон розподілу Стьюдента (його ще називають t-розподілом). Він задається в такий спосіб. Нехай випадкова величина Z має стандартний нормальний розподіл N(0,1), а випадкова величина не залежить від Z і розподілена за законом  з r ступенями волі, тоді випадкова величина

має закон розподілу Стьюдента з r ступенями волі. Він задається формулою

 ,

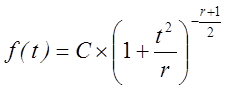де C - константа.

Закон розподілу Стьюдента симетричний щодо нуля - свого середніх. Коли , випадкова величина прагне до свого граничного значення, що буде мати стандартний нормальний закон розподілу, тобто .

Визначення.  Під статистичною гіпотезою будемо розуміти логічне висловлення про значення досліджуваних параметрів.

Наприклад, запис виду

                                           (4.1)

позначає висування гіпотези про те, що деякий параметр  приймає гіпотетичне значення . Вираження (4.1) називають нульовою гіпотезою. Альтернативне висловлення представляє вираження

 .                                          (4.2)

Вираження (4.2) називають двосторонньою альтернативною гіпотезою.

4.1.2. Етапи перевірки гіпотез

Відповідно до загальної схеми перевірки статистичних гіпотез нульова гіпотеза при двосторонній альтернативній гіпотезі перевіряється по наступним кроках.

Крок 1. Формулювання нульової й альтернативної гіпотез.

Крок 2. Вибір статистики, за значеннями якої судять про справедливість нульової гіпотези. Під статистикою розуміється деяка функція від випадкових величин з відомим законом розподілу.

Крок 3. Формулювання правила перевірки гіпотези і визначення необхідного обсягу вибірки. При цьому повинні бути задані рівень довіри і величина, зв'язана з потужністю критерію. Можна надходити інакше, задавши рівень довіри й обсяг вибірки і мінімізувати потужність критерію.

Крок 4. У залежності від гіпотези, що перевіряється, і її альтернатив вибираємо одне- чи двосторонню перевірку. Знаходимо область прийняття нульової гіпотези.

Крок 5. Порівнюємо розраховану величину статистики з її теоретичним значенням і приймаємо рішення про чи прийняття відхиленні гіпотези.

Крок 6. Інтерпретуємо результати перевірки гіпотез.

4.1.3. Приклад

Ґрунтуючись на вихідних даних результатах розрахунків приклада п. 3.3, виконати перевірку гіпотез про значимість параметрів  і  рівняння (3.8).

Рішення

Досліджуємо значимість параметра .

Крок 1. Нульову й альтернативну гіпотези приймемо у виді

Зміст гіпотез полягає в тому, що фактично передбачається перевірити, чи істотно ні вплив рівня фондоемкости продукції на витрати на одиницю продукції.

Крок 2. Як статистику можна узяти функцію виду 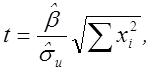 яка відповідно до результатів п. 4.1.1 має t-розподіл з (n-2) ступенями волі.

Крок 3. Правило перевірки нульової гіпотези складається в зіставленні емпіричного значення t-критерію з теоретичним. Обсяг вибірки дорівнює 10. Рівень довіри припускаємо рівним 95 %. Теоретичне значення t-критерію одержуємо зі статистичних чи таблиць за допомогою функції EXCEL СТЬЮДРАСПОБР(0,025; 8). Воно дорівнює 2,751531.

Крок 4. Вибираємо двосторонню перевірку ( ). У цьому випадку область прийняття нульової гіпотези має вид:

 .

За результатами розрахунків, представленим у таблиці 3.1, маємо:

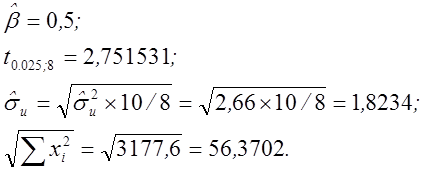
Звідси інтервал прийняття нульової гіпотези виглядає в такий спосіб

 .

Крок 5. Перевіряємо приналежність величини  нашому інтервалу і переконуємося в тім, що це значення не попадає в область прийняття нульової гіпотези. Отже, з імовірністю, не меншої 95 %, нульову гіпотезу відхиляємо і переходимо до перевірки альтернативної гіпотези.

Крок 6. Таким чином, параметр  значимий відрізняється від нуля. Останнє означає, що фактор фондоемкости істотно впливає на витрати, що приходяться на одиницю продукції.

Досліджуємо тепер значимість параметра .

Крок 1. Нульову й альтернативну гіпотези представимо у виді

Зміст гіпотез полягає в тому, що необхідно перевірити, не істотність впливу постійно діючих факторів на витрати на одиницю продукції.

Крок 2. Як статистику можна узяти функцію виду  яка відповідно до результатів п. 4.1.1 має t-розподіл з (n-2) ступенями волі.

Крок 3. Правило перевірки нульової гіпотези складається в зіставленні емпіричного значення t-критерію з теоретичним. Обсяг вибірки дорівнює 10. Рівень довіри припускаємо рівним 95 %. Теоретичне значення t-критерію одержуємо зі статистичних чи таблиць за допомогою функції EXCEL СТЬЮДРАСПОБР(0,025; 8). Воно дорівнює 2,751531.

Крок 4. Вибираємо двосторонню перевірку ( ). У цьому випадку область прийняття нульової гіпотези має вид:

 .

За результатами розрахунків, представленим у таблиці 3.1, маємо:

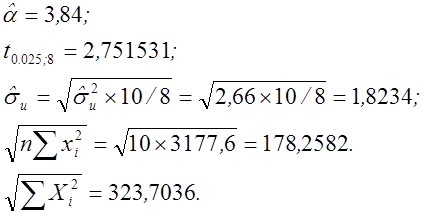
Звідси інтервал прийняття нульової гіпотези виглядає в такий спосіб

 .

Крок 5. Перевіряємо приналежність величини  нашому інтервалу і переконуємося в тім, що це значення попадає в область прийняття нульової гіпотези. Отже, з імовірністю, не меншої 95 %, нульову гіпотезу приймаємо.