Предмет, метод і задачі курсу «Економетрія». Основи економетричного моделювання. Найпростіша лінійна економетрична модель. Загальна лінійна модель, страница 7

Крок 6. Таким чином, параметр  не значимий відрізняється від нуля. Останнє означає, що постійні фактори не істотно впливають на витрати, що приходяться на одиницю продукції. Виходить, виявляється можливим розглядати іншу регресійну модель виду .

4.2. Оцінка адекватності моделі

4.2.1. Небагато теорії

У дійсному посібнику основна увага приділяється лінійним регресійним моделям. Тому оцінку адекватності моделі розуміємо як перевірку наявності лінійного зв'язку між факторами X і Y.

Перевірка адекватності моделі може бути проведена за допомогою коефіцієнта детермінації і статистики, побудованої на його основі [5, 7]. Оцінка коефіцієнта детермінації має вид

 ,

де .

Можна показати, що випадкова величина (будемо позначати її через F)  задовольняє закону розподілу Фишера з (1; n-2) ступенями волі. Вона може бути задіяна як статистику при перевірці гіпотези про адекватність лінійної моделі.

Нульова гіпотеза про відсутність лінійного зв'язку між факторами X і Y має вид

 .

Перевірку цієї гіпотези виконують виходячи з нерівності

 ,                                                               (4.3)

виконання якого на 100×ε  % рівні значимості вимагає відхилення нульової гіпотези. Величина  береться зі статистичних чи таблиць розраховується за допомогою функції FРАСПОБР(0,05;1;n-2) електронної таблиці EXCEL.

4.2.2. Приклад

Потрібно перевірити адекватність моделі , побудованої в прикладі п. 3.3.

Рішення

Спочатку розрахуємо R² . Величини , знаходяться в передостанньому стовпці і передостанньому рядку, в останньому стовпці і передостанньому рядку табл. 3.1 відповідно. Вони рівні 26,60 і 819,60. Тоді R² = 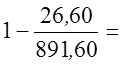0,965746.

Емпіричне значення F-критерію дорівнює

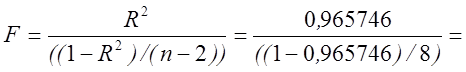 238,502.

Теоретичне значення F-критерію  одержуємо за допомогою функції FРАСПОБР(0,05;1;n-2) електронної таблиці EXCEL:

 = FРАСПОБР(0,05;1;8) = 5,317645.

Підставляємо знайдені значення в нерівність (4.3) і переконуємося, що воно виконано. Отже, з імовірністю, не меншої 95 %, можна затверджувати, що модель  адекватно описує вплив рівня фондоемкости на  витрати на одиницю продукції.

4.3. Короткі висновки

1. Нульова й альтернативна гіпотези, застосовувані для оцінки значимості параметрів найпростішого рівняння парної лінійної регресії, мають вид:

для параметра  і

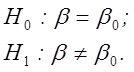
для параметра .

2. Гіпотези про значимість параметра  й адекватності моделі парної лінійної регресії можна представити у формі:

3. Для перевірки гіпотез використовують t-критерій Стьюдента і F-критерій Фишера.

4. У загальному випадку процедура перевірки гіпотез складається із шести кроків.

4.4. Питання до теми 4

1.  Які закони розподілу випадкових величин використовуються в процедурах перевірки гіпотез?

2.  Що таке статистична гіпотеза?

3.  У чому полягає розходження між нульовою й альтернативною гіпотезами?

4.  Назвати етапи перевірки гіпотез.

4.5. Задачі для самостійного рішення

Використовуючи результати рішення свого варіанта завдання з п.3 (табл. П1 на стор. 43), перевірити значимість параметрів рівняння регресії й адекватність моделі при 95 % рівні довіри.

4.6. Основні терміни і поняття

Статистика Закон розподілу Стьюдента Закон розподілу Фишера

Статистична гіпотеза Нульова гіпотеза Альтернативна гіпотеза

Тема 5. Загальна лінійна модель

5.1. Уведення. Припущення

Розгляд найпростішої двухфакторной моделі, методів дослідження, властивостей охоплює лише елементарні економічні ситуації. Більш реальними є эконометрические моделі, що включають кілька факторів.

Будемо виходити з того, що з метою дослідження лінійного зв'язку між результуючим фактором Y і пояснюючими k-1 факторами X₂, …, X_k  було виконано статистичне спостереження. У результаті спостереження зареєстрована вибірка обсягу n, що представимо таблицею виду (табл. 5.1)

Припустимо, що існує лінійний зв'язок між Y і факторами X₂, …, X_k виду:

,                              (5.1)

Таблиця 5.1

Спостереження факторів

№ п/п	Y	X2	X3	…	Xk
1	Y1	X12	X13	…	X1k
2	Y2	X22	X23	…	X2k
…	…	…	…	…	…
n	Yn	Xn2	Xn3	…	Xnk

де доданок U відбиває вплив на інших факторів, помилки вимірів, помилки вибору типу моделі. Це припущення назвемо гіпотезою лінійності. Тоді для спостережених величин (табл. 5.1) можна записати

                        (5.2)

У системі рівнянь (5.2) коефіцієнти і параметри розподілу для випадкових величин U_i невідомі і повинні бути оцінені. У цьому складається одна з задач, які необхідно вирішувати.

Систему (5.2) запишемо в матричній формі:

 ,                                            (5.3)

де

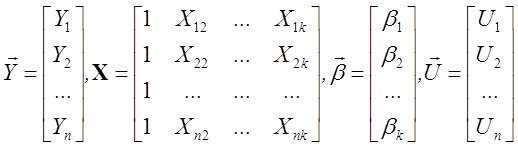 .                 (5.4)

У позначеннях (5.4) матриця спостережень X містить стовпець, що складається з одиниць. Цей стовпець відноситься до вільного члена . Матрицю  називають матрицею регрессоров.

Для одержання оцінок вектора приймемо ряд припущень щодо способу одержання спостережень. У залежності від зроблених припущень чи розробляються підбираються методи оцінювання.

Основні і найбільш прості гіпотези поряд з гіпотезою лінійності (5.1) наступні:

 ;                                            (5.5)

 ;                                     (5.6)

 - матриця фіксованих чисел;                     (5.7)

                                         (5.8)

.                                      (5.9)

Гіпотеза (5.5) означає, що  для всіх i , тобто що випадкові перемінні Ui мають нульове математичне чекання.

Гіпотеза (5.6) дуже важлива в тім змісті, що вона відбиває сукупність властивостей ковариационной матриці I_n - одинична матриця розмірності n. У цій гіпотезі виражені властивості, виконання яких ми вимагаємо. Перше: - це властивість некоррелированности випадкових величин ; друге:  для всіх i - властивість сталості дисперсії випадкових величин U_i , називане гомоскедастичностью.