Теплофизические свойства твердых тел

2.2. ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ

Комплекс физических свойств, относимых к тепловым, включает теплоемкость твердых тел, их тепловое расширение, теплопроводность и температуропроводность. Теплофизические характеристики материалов предопределяют выбор и ведение важнейших технологических процессов при производстве и обработке практически всех неметаллических и металлических материалов. Сюда относятся сушка, обжиг, закалка, размягчение, плавление, спекание - основные энергоемкие процессы формирования получаемых структур и изделий, связанные с тепловым воздействием. Теплопередача может осуществляться радиационным путем, конвекцией и с помощью теплопроводности.

Понимание физической сути явлений и процессов, происходящих в твердом теле в процессе его нагревания - обязательное условие грамотного ведения тепловой обработки материалов.

2.2.1. Нормальные колебания решетки и их дисперсия

В твердом теле любого типа атомы и молекулы при любой температуре, включая 0К, находятся в колебательном движении около их положения равновесия. Эти колебания при не слишком высоких температурах (и амплитудах колебания) можно считать гармоническими. Энергия, сосредоточенная в теле в виде энергии колебательного движения, довольно значительна. Этот вид энергии весьма динамичен - тело способно легко воспринимать такую энергию или отдавать в процессе нагрева или теплообмена с окружающими телами. В молекулярных кристаллах картина атомных движений усложняется как возможностью крутильных колебаний молекул, так и колебаниями атомов внутри молекул.

Следствием сильного межатомного взаимодействия в конденсатах является обязательная передача соседям возбуждения, полученного одним атомом. Колебание, возбужденное у одной частицы, немедленно (со скоростью продольной волны) передается соседним частицам и в твердом теле возбуждается коллективное движение в виде упругой гармонической волны, охватывающей все тело. Такое коллективное движение  атомов кристалла называется   н о р м а л ь н ы м 

 к о л е б а н и е м   р е ш е т к и. В силу существования разных межатомных расстояний, во всяком теле присутствует совокупность взаимодействующих упругих волн различного типа и различной длины. В твердом теле ограниченных размеров при данной температуре устанавливается стационарное состояние колебаний, которое можно описать как суперпозицию стоячих воли, для которых поверхности тела играют роль узловых точек (по крайней мере, для волн с частотами звукового диапазона).

В теле с числом частиц N и, соответственно, числом степеней свободы 3N, могут возникнуть 3N нормальных колебаний.

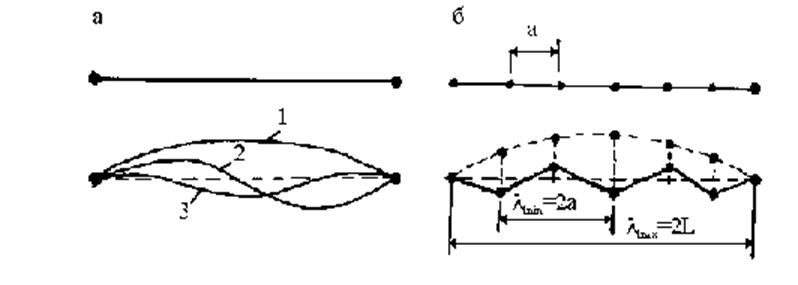
Рассмотрим основные представления теории колебаний в трехмерном кристалле на одномерной модели (рис.2.2.1). Будем вначале рассматривать одномерную атомную цепочку как струну с равномерным распределением линейной плотности вещества, а затем учтем ее дискретное строение. Если закрепить концы струны (рис. 2.3.1,а), то в ней можно наблюдать ряд стоячих волн с узлами и пучностями, соответствующих первой, второй, третьей и т.д. гармоникам.

В атомной цепочке  возможно также выделение гармоник колебаний, причем самая короткая длина волны, которая может существовать в такой структуре, соответствует (рис. 2.2.1,б)

l_min = 2a,                                                                                   (2.2.1)

а максимальная длина волны

l_max = 2L,                                                                                  (2.2.2)

где a - минимальное  расстояние между  атомами (параметр решетки в трехмерном  кристалле или просто l_min в аморфном твердом теле), L  - максимальный макроскопический размер тела.

В энергетическом спектре любого тела наибольший вклад принадлежит высокочастотным    колебаниям. Поскольку круговая частота колебаний связана с другими параметрами волны соотношениями             

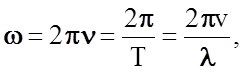                                                            (2.2.3)

где n - частота колебаний, Т – период колебаний, v – скорость волны и l - ее длина, то для максимальной частоты колебаний в решетке, состоящей из идентичных атомов, можно записать соотношение 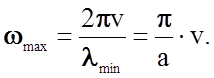(2.2.4)

В уравнении (2.2.4) v имеет смысл максимальной скорости продольной волны v_l -  скорости звука в твердом теле. Ясно, что в любом кристалле w_max является константой материала. Например, для MgO в направлении [100] a = 2,2×10^-10 м,  v_l = 9361 м/с,  следовательно, w_max » 1,4×10¹⁴ c^-1. Близкие к указанному для MgO значения характерны и для других твердых тел (~10¹³ c^-1…10¹⁴ c^-1).           

Рис. 2.2.1. Колебания струны (а) и одномерной атомной цепочки (б)

При описании волновых процессов в твердых телах часто пользуются волновым  вектором , модуль которого равен

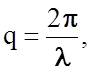                                                                                                                  (2.2.5)

где l - длина волны колебаний. Направление совпадает с направлением распространения колебаний.

Поскольку из (2.3) 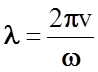  , то

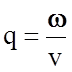  или  w = qv                                                               (2.2.6)

Формула (2.2.6),  описывающая связь между частотой волны w (или ее длиной  l), волновым вектором  и скоростью v представляет собой дисперсионное соотношение. Соответствующие графики (рис.2.2.2) называются   д и с п е р с и о н н ы м и   к р и в ы м и. При возрастании   от 0 до p/a  круговая частота  соответственно увеличивается, достигая максимального значения.

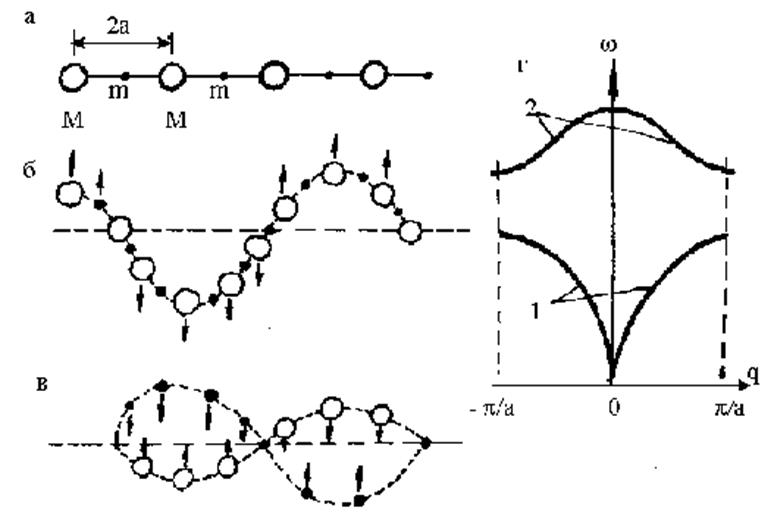
Интересен в практическом смысле случай колебаний одномерной цепочки, состоящей из разнородных правильно чередующихся атомов или ионов (рис.2.2.3,а), Пусть масса атомов (ионов) различна - M и m. Это может быть, например, цепочка из ионов Na⁺ и Cl ^-.

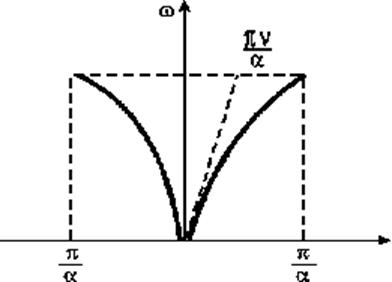Рис.2.2.2. Дисперсионные кривые для тепловых колебаний одномерной атомной цепочки. Пунктир – для однородной струны

Рис. 2.2.3. Колебания неоднородной атомной цепочки (а,б,в) и соответствующие им дисперсионные кривые (г) (1 - акустическая ветвь, 2 - оптическая ветвь)

В такой цепочке возможно возникновение колебаний двух типов (рис.2.2.3,б,в). Колебания, заключающиеся в совместном смещении атомов обоих сортов (рис. 2.2.3,б) ничем не отличаются от изображенных на рис.2.2.3,а, соседние атомы колеблются в практически одинаковой фазе. По частотам они включают весь интервал от 0 до 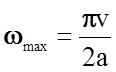    при изменении q от 0 до . Такие колебания называются  а к у с т и ч е с к и м и, на графике рис. 2.2.3,г они изображены кривыми 1. Именно они играют определяющую роль в тепловых свойствах твердых тел - теплоемкости, теплопроводности, термическом расширении.

Однако возможен другой случай (рис.2.2.3,в), когда соседние  атомы колеблются в противофазах. Такие колебания являются более высокочастотными по сравнению с акустическими (рис. 2.2.3,г, кривая 2), носят название  о п т и ч е с к и х   и играют основную роль при взаимодействии решетки со светом. Из анализа графиков (рис.2.2.3,г) следует, что при q = 0  w_ак = 0, а w_опт достигает максимума, и при 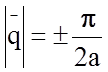 частота w_опт оптических колебаний уменьшается до минимума, в то время как  w_ак максимальна.