Теплофизические свойства твердых тел, страница 11

где z - постоянная интегрирования, а интеграл, подобно решению теплофизической задачи, называют интегралом ошибок Гаусса, в данном случае его следует обозначить  .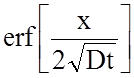

Уравнение (2.58) переписываем в форме

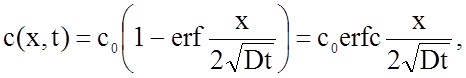                          (2.2.59)

здесь егfс - сокращенная форма записи дополнительной функции (1 -erf). Функции егf и erfc табулированы (см. например, “Справочник по специальным функциям” -М.: Наука, 1979, с. 131). Уравнение (2.2.59) хорошо описывает распределение примесных атомов по глубине при диффузии не только из конденсированной, но также из паровой и газовой фазы. Графические решения уравнения (2.2.59) в виде функции c/c₀ = f(x,t)  представлены для трех значений времени на рис.2.2.15.

Для точного определения величины основного параметра диффузии – коэффициента D, из эксперимента, например, с применением метода меченых атомов, определяется вид концентрационной зависимости c/c₀ = f(x), из которой для определенной глубины х определяют с/с₀. Это соответствует  определению частного значения функций 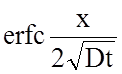   и, следовательно, erf. Зная эти значения, определяют из таблиц величину 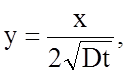  откуда, при известных x и t, легко найти величину коэффициента диффузии D при данной температуре .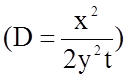

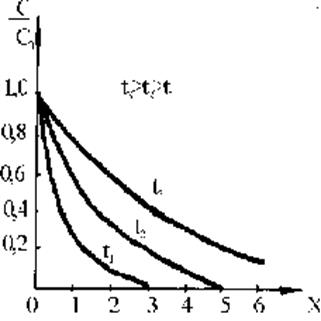Рис.2.2.15.Распределение относительной концентрации диффундирующего вещества от глубины диффузии при различной продолжительности процесса (t₃ > t₂ > t₁) и одинаковой температуре (диффузия из постоянного источника)

Можно заметить, что примерно половина относительного насыщения достигается, когда безразмерный параметр 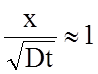 . Этот факт позволяет грубо оценивать ход процесса диффузии, если величина D  для условий процесса известна. Решение уравнения (2.58) получено для диффузии в пластинку конечной толщины, в цилиндр и в шар. Для оценочных расчетов полезно запомнить, что насыщение практически завершается (достигает более 98%), когда  для пластинки, для цилиндра и  для шара, где L  - толщина пластинки, радиус цилиндра или радиус шара соответственно.

2.2.8.1.2. Одномерная диффузия из непостоянного источника

Пусть источник толщиной h (слой краски, напыленный слой металлического проводника, полупроводника, диэлектрика и т.д.) расположен на поверхности x = 0 полубесконечного тела. Существенным отличием от первого случая является возможность истощения источника. Начальное распределение диффундирующего элемента задано в виде

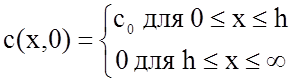
Если h достаточно мало (в принципе h®0), то решение второго уравнения Фика запишется в виде

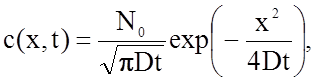                                                (2.2.60)

где N₀ = c₀h - начальное количество, содержащееся в слое единичной площади. Графические решения уравнения (2.2.60) представлены схематически на рис.2.2.16 для различной продолжительности t(t₃>t₂>t₁)   процесса при постоянной температуре. Вследствие истощения источника концентрация диффундирующего вещества в поверхностном слое (x=0) уменьшается с увеличением продолжительности процесса.

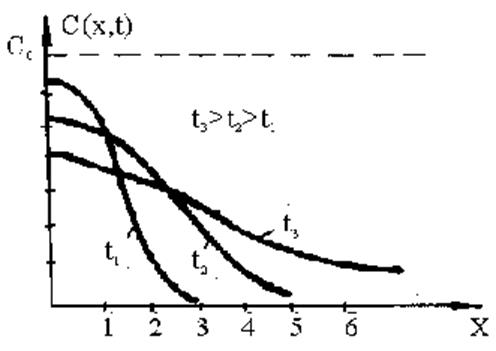
Рис.2.2.16.Зависимость концентрации  от глубины при диффузии         из непостоянного источника при постоянной температуре процесса в раз  личные моменты времени

2.2.8.1.3. Температурная зависимость коэффициента диффузии. Энергия активации диффузии

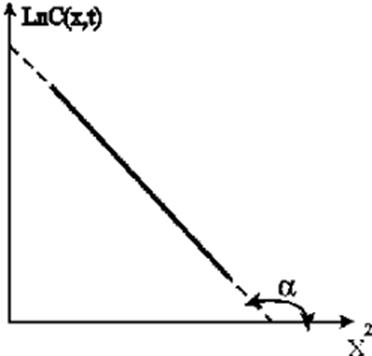
Уравнение (2.2.60) позволяет на основе экспериментальных данных построить графическую зависимость ln c(x,t)  от x² в виде прямолинейной зависимости в полулогарифмических координатах (рис.2.2.17).

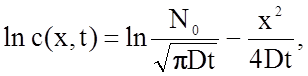Действительно,  так что угол наклона a может быть определен. Поскольку 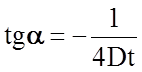, то, зная a и продолжительность t процесса диффузии, найдем величину коэффициента диффузии D при данной температуре.

          Рис.2.2.17.График функции, описываемой формулой (2.2.58) в  полулогарифмических координатах

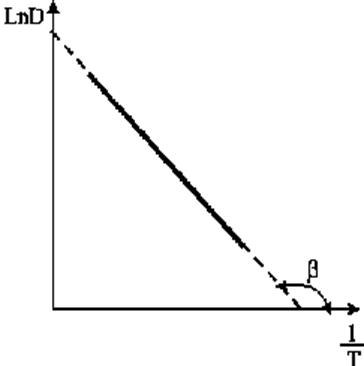
Рис.2.2.18.Зависимость коэффициента диффузии от обратной температуры

Вычислив коэффициенты D  при нескольких температурах, можно построить график температурной зависимости коэффициента, диффузии в координатах 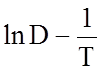 (рис.2.2.18), из которого следует факт, что величина коэффициента диффузии, подобно константе скорости химических реакций, подчиняется уравнению Аррениуса:

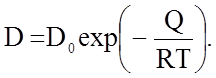                                                              (2.2.61)

Причем из графика (рис.2.2.18) можно найти величину энергии активации процесса диффузии  Q, поскольку 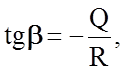  R - универсальная газовая постоянная. Наконец, зная Q,  можно определить и D₀ из уравнения (2.2.61).Установлено также, что предэкспоненциальный множитель D₀ изменяется в относительно узком интервале от 10^-6  до 10^-4 м²/с, а величина энергии активации Q самодиффузии для многих элементов грубо может быть определена из соотношения

Q = 18 RT_пл,                                                                           (2.62)

где T_пл - температура плавления. Например, для золота (T_пл=1336 К) при расчете по ф.(2.62) Q составляет 2×10⁵ Дж×моль^-1, а в эксперименте с мечеными атомами получено  Q = 1,9×10⁵ Дж×моль^-1, что следует признать очень хорошим совпадением. Коэффициенты диффузии D в твердых телах очень малы при комнатной температуре, например, у того же золота коэффициент самодиффузии составляет только около 10^-35 м²/с.

2.2.8.1.3. Особенности диффузии в различных оксидных системах и других твердых телах

Параметры диффузии, определяемые обычно при высокотемпературных измерениях, имеют определяющее значение для понимания разнообразных технологически важных процессов, протекающих в твердых телах, поскольку они позволяют судить о подвижности атомов и дефектов кристаллической решетки.

Проведение обширных и тщательных измерений коэффициентов диффузии для щелочно-галоидных кристаллов, а также электропроводности в широком интервале температур позволило выявить механизм протекания диффузионных явлений в кристаллах с ионной связью.

Эксперименты, проведенные различными авторами с кристаллами хлористого натрия, показывают, что на графике зависимости коэффициента диффузии от температуры имеются два участка (рис. 2.2.19). Причем, в области высоких температур, иногда называемой областью собственной диффузии, данные для различных образцов, полученные разными авторами, оказываются близкими.