Теплофизические свойства твердых тел, страница 5

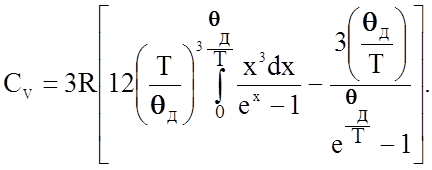
Применительно к гетерофазным структурам, таким, как спеченные инструментальные материалы, пористая керамика, огнеупоры, бетон, кирпич, природные каменные материалы, зачастую содержащие связанную воду, понятие молярной теплоемкости мало применимо. В практических расчетах используется величина удельной теплоемкости С как количество теплоты, которое необходимо сообщить 1 кг вещества, чтобы повысить его температуру на один градус (^oC или К). Теплоемкость неорганических материалов (кирпич, керамика, сырье из природных материалов, бетон) изменяется в пределах 0,75…0,92 кДж/(кг×град). Очень сильно на теплоемкость материалов влияет присутствие воды, так как для нее С = 4,19 кДж/(кг×град).

Исследования теплоемкости твердых тел, с одной стороны, позволяют рассчитывать теплотехнические параметры технологического оборудования и расхода энергии для производства материалов и их последующей обработки, с другой - изучать влияние на структуру и фазовый состав различных добавок и особенностей технологии производства.

2.2.5. Тепловое расширение твердых тел.

2.2.5.1. Термический коэффициент линейного расширения (ТКЛР)

Представление о строго гармоническом законе колебаний решетки является лишь первым приближением, удобной моделью при описании  теплоемкости твердых тел. Однако оно является непригодным при описании таких физических явлений, как тепловое расширение и теплопроводность. В частности, тепловое расширение тел и связанное с ним возникновение технологических и остаточных внутренних напряжений в изделиях, подвергнутых термической обработке, можно понять и теоретически проанализировать только учитывая отклонения закона колебаний частиц от гармонического закона, т.е. ангармоничность колебаний.

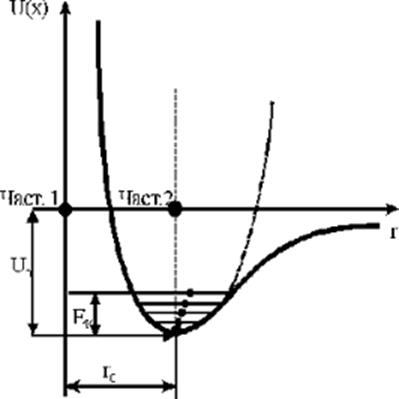
При абсолютном нуле, если не учитывать слабые нулевые колебания, ионы решетки располагаются на равновесных расстояниях  r=r₀=a друг от друга, занимая место на дне потенциальной ямы в состоянии U₀ = U(r₀). Размеры тела при этом минимальны. При повышении температуры размеры всех конденсированных тел, твердых и жидких, увеличиваются (аномалии, в частности, для воды, объясняются или фазовыми перестройками или изменениями характера межатомных связей). Для количественного описания этого явления привлекаются представления об асимметрии потенциальной ямы (рис. 2.8) и ангармоничности колебаний ионов около узлов кристаллической решетки.

Если бы потенциальная яма была параболически - симметричной, то потенциальная энергия одномерных, вдоль оси Х, колебаний системы из пары частиц описывалась бы формулой 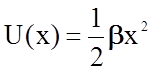 , а сила взаимодействия частиц была бы равна

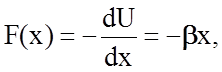
что представляет собой известный закон Гука  (x=çr – r₀ç - смещение частицы  2, отсчитываемое от закрепленной частицы 1). Известно, что в этом случае частицы совершают гармонические колебания около неподвижных положений равновесия и тепловое расширение не должно наблюдаться.

Причины теплового расширения можно понять, рассматривая тот же классический осциллятор, если в выражении для потенциальной энергии учесть ангармонические члены:

U(x) = -U₀ + bx² – gx³ + fx⁴,                                                (2.2.31)

где

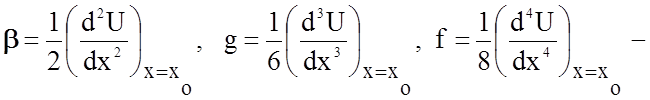
константы, член с x³ описывает асимметрию взаимного отталкивания атомов, член c x⁴ – сглаживание колебаний при больших амплитудах, свойственных жидкому состоянию (его мы можем пока опустить). Квазиупругая сила межатомного взаимодействия в такой простой двухатомной модели равна

F(x) = - bx + gx².                                                                   (2.2.32)

При увеличении температуры кинетическая энергия частиц тела увеличивается, при этом одновременно с изменением уровня энергии наблюдается смещение положения равновесия частиц в сторону увеличения межатомных расстояний (см. точки на рис.2.2.8). Ангармонизм колебаний проявляется как увеличение смещений частицы 2 вправо от частицы 1 по сравнению со смещением влево. В уравнении (2.2.31) это учтено ненулевым коэффициентом g, называемым коэффициентом  ангармоничности.

Оценим теперь количественно величину коэффициента теплового расширения a и его зависимость от температуры и параметров нагреваемого материала. При любой неизменной температуре в состоянии равновесия средняя сила, действующая на любую частицу, равна 0 (`F(x)  = 0), колебания происходят около некоторого равновесного положения (r<sub>0</sub> + `x), определяемого из соотношения

F(`x )  = - b`x  + g`x ².                                                        (2.2.33)

Если в первом приближении пренебречь вкладом gx³ в величину потенциальной энергии колебаний ввиду малости x - отклонения от положения равновесия в сравнении с r₀ (`x  = r – r₀), то потенциальную энергию колебаний можно положить равной

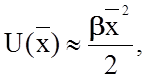   откуда 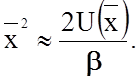                                    (2.2.34)

Подставим (2.34) в (2.33) и определим величину `х:

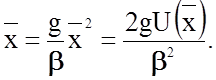          (2.2.35)

В произвольной точке траектории колеблющейся частицы полная энергия колебаний Е состоит из кинетической и потенциальной энергий, причем средние значения энергий равны (), поэтому полная энергия колебания Е = . Полагая теперь , определим среднее смещение положения равновесия `х колебаний частиц через полную энергию колеблющейся системы  Е:

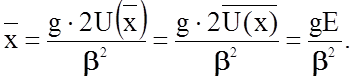                                          (2.2.36)

Относительная деформация e  вследствие одномерного удлинения межатомной связи равна

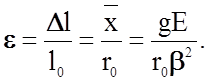                                                               (2.2.37)    

Термический коэффициент линейного расширения (ТКЛР) по физическому смыслу есть 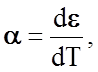, откуда

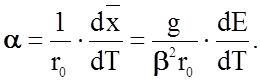                                                        (2.2.38)

Рис.2.2.8. Потенциальная кривая взаимодействия двух частиц. Точками показаны положения равновесия при различных значениях кинетической энергии Е_К  (с ростом температуры). Пунктир - параболическая зависимость

Величина 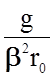 является константой для данного материала и вообще величина, близкая для всех твердых тел, 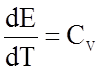 - теплоемкость, отнесенная к одной частице (хотя, в термодинамическом смысле это неправомерно, однако принципы вывода величины a не изменяются и при анализе поведения трехмерной системы из N частиц). Специально проведенными исследованиями показано, что с повышением температуры коэффициент линейного термического расширения увеличивается в 3...4 раза в интервале 100...300К, повторяя ход кривой С_V = C_V(Т) (см. рис.2.2.6,а), а при более высоких температурах остается постоянным и составляет для всех тел величину примерно 10^-5...10^-4 град ^-1. При практическом использовании ТКЛР для технологических расчетов необходимо иметь в виду: