Теплофизические свойства твердых тел, страница 4

Полную энергию решетки можно получить, проинтегрировав (2.2.23) по частотам от w =0 до w = w_max, причем  w_max = w_Д, - частоте Дебая, если температура кристалла  Т³q_Д. К результату интегрирования следует еще добавить "нулевую" энергию Е₀, которая по Дебаю для одного моля равна

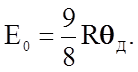                                                                         (2.2.24)

Подставим в формулу (2.2.23) значение Е_н.к. из уравнения (2.2.17), r(w) - из соотношения (2.2.10) и в предположении, что Т³q_Д для одного моля (N = N_A) кристалла, получим

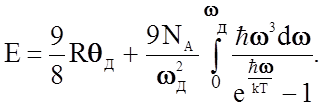                                               (2.2.25)

В формуле (2.2.25) подставлено r(w)  в виде 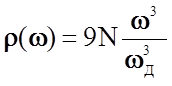, что

получено  подстановкой в (2.2.10) значения v из формулы (2.2.12).

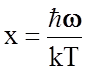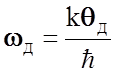Если в формуле (2.2.25) перейти к безразмерной переменной   и вспомнить, что , а 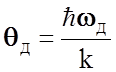, то, опуская промежуточные выкладки, можно записать  

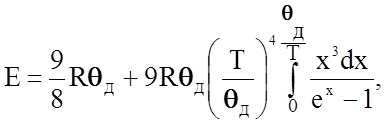                                      (2.2.26)

что после дифференцирования по Т дает величину молярной теплоемкости кристалла                

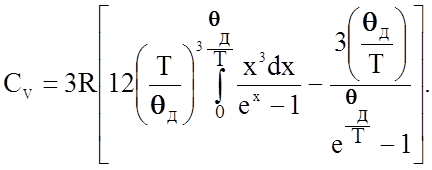          (2.2.27)

Последняя формула в пределе малых значений Т (Т<<q_Д) дает (с учетом, что при  Т<<q_Д интеграл )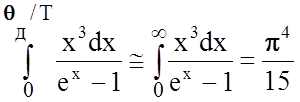

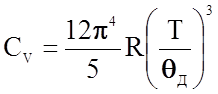            ~T³.                                      (2.2.28)

Формула (2.2.28) хорошо соответствует экспериментальным данным, полученным при исследовании твердых диэлектриков в области низких температур.

В области высоких температур 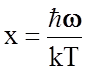 мало, поэтому в первом приближении можно считать e^x » 1+x, что упрощает выражение (2.2.27) до C_V » 3R » 6 кал/(моль×град) = 25 Дж/(моль×град). Этот предельный случай, соответствующий закону Дюлонга и Пти, мы уже получали.

Графически зависимости молярной теплоемкости от относительной температуры T/q_Д представлены на рис.2.2.6. Следует отметить, что, по данным многих измерений, молярные теплоемкости различных кристаллических и аморфных тел простой структуры с большой точностью совпадают с предсказанной по теории Дебая (рис. 2.2.6,а). Лишь в области температур вблизи абсолютного нуля наблюдаются отклонения от закона Дебая для металлов, что объясняется присутствием в металлах электронного газа

Рис.2.2.6. Зависимости теплоемкости от температуры по различным теориям в сравнении с экспериментом (а, кружки), и особенности теплоемкости решетки и электронного газа в металлах вблизи абсолютного нуля (б)

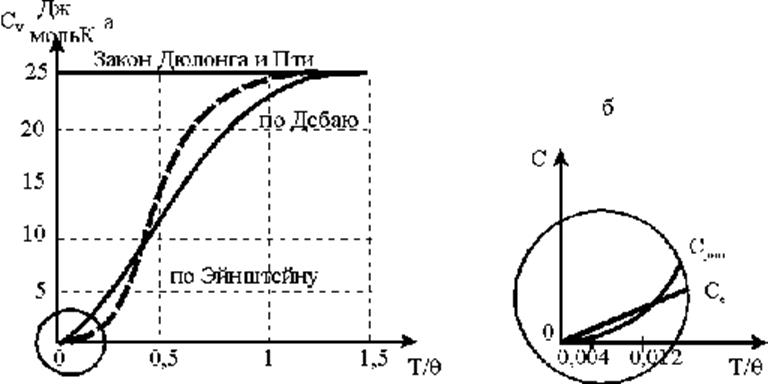Вместе с тем, малое отличие теплоемкости металла от той, что предсказывает теория Дебая, рассматривающая лишь колебания решетки и вообще не учитывающая наличие свободных электронов, подтверждает уже высказанное выше (ч.1) утверждение о возможности участия в тепловом движении лишь ничтожного количества электронов, находящихся на энергетических уровнях, непосредственно прилежащих к уровню Ферми.

Вклад в теплоемкость электронов становится заметным лишь на фоне малого вклада решеточной теплоемкости в окрестности абсолютного нуля.

2.2.4.2. Полуэмпирические соотношения для теплоемкости реальных тел с дефектной структурой

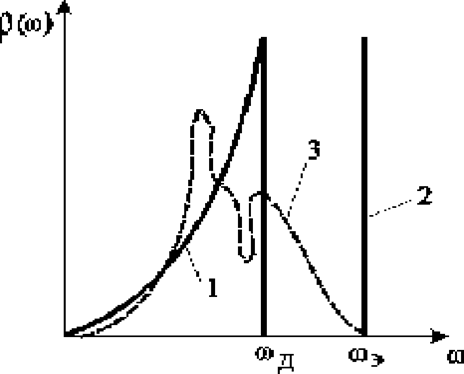
Если сравнивать экспериментальные данные о спектральных характеристиках тел с приближениями Эйнштейна и Дебая для спектральной функции  r(w) (рис.2.2.7), то можно понять, почему наиболее точные ответы теории дают лишь при предельных значениях высоких и очень низких температур.

Спектры колебаний реальных решеток существенно богаче и явно не укладываются в рамки простого параболического приближения Дебая и тем более - точечного приближения Эйнштейна.

Однако показано, что подстановка в исходную формулу (2.2.23) истинного вида функции  r(w), обычно вычисляемой с помощью ЭВМ на основе экспериментальных данных или более реалистичных теоретических законов дисперсии, приводит к хорошему совпадению экспериментальных и теоретических результатов для теплоемкости и энергии тепловых колебаний решетки в широком интервале температур. Вместе с тем из опыта известно, что спектральная функция и теплоемкость очень чувствительны к таким характеристикам, как структура, химический состав тела, его дефектность. Например, при Т=100К теплоемкости углерода в графитной и алмазной фазе отличаются приблизительно в 7 раз, а при Т = 50К - уже в 23 раза. При фазовых переходах в твердой фазе (например, ромбической серы в моноклинную, превращения в кристаллах силикатов и многие другие), теплоемкость изменяется скачком, что послужило основой весьма точного метода дериватографического анализа  (ДТА) определения температуры фазового превращения.

Рис.2.2.7. Зависимость  частотного спектра; 1 - приближение Дебая, 2 - приближение Эйнштейна, 3 - истинный спектр колебаний решетки (качественно)

Установлено также, что в реальных слоистых, зернистых и волокнистых структурах теплоемкость может значительно отклоняться от закона Дебая пропорциональности Т³ вследствие различного характера взаимодействия атомов внутри блока - зерна, слоя, волокна - и между слоями, зернами, волокнами. В этом случае простая замена суммирования энергии по частотам интегрированием в широком интервале частот оказывается неправомочной из-за наличия разрывов в функции  r(w).

Для получения точных значений энергии и теплоемкости приходится вычислять функцию теплоемкости "по кускам" в разных температурных интервалах, вводить эмпирические коэффициенты или представлять зависимость в виде полиномов и сумм. В частности, для слоистой структуры графита  (слои, состоящие из шестиатомных колец, связанных друг с другом, располагаются в плоскостях, параллельных Oxy, ось z  перпендикулярна им) получено соотношение:

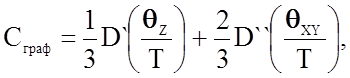                                           (2.2.29)

где q_Z = 950К - температура Дебая для межслойных связей, q_XY = 2500К - для внутрислойных связей. Величины D'  и D" вычисляются  интегрированием  

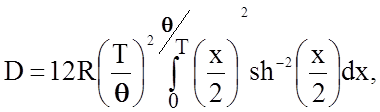
где 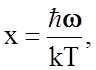 а величина  q = q_Z при определении D`  и q = q_XY при вычислении D``.

Попытки получения аналитических выражений для теплоемкости реальных некристаллических структур также связаны с построением двух- и многопараметровых зависимостей.

Например, для метасиликатного стеклообразного натрия Na₂SiO₃ Тарасовым В.В. с сотрудниками получено соотношение

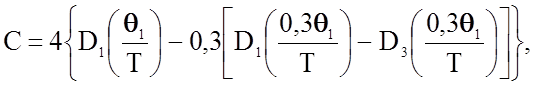                (2.2.30)

где  q₁ = 1323К,

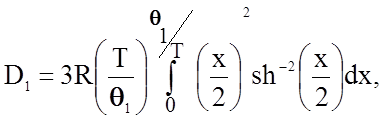
D₃  - функция Дебая