Действительно надежные данные получают обычно экспериментально, в лабораторных исследованиях, и представляют в виде графиков и таблиц значений l при различных температурах, причем погрешность производимых измерений достигает в лучших случаях 2...5%.
Качественно порядок величины l и характер температурной зависимости может быть объяснен с позиций фононной теории для диэлектриков; при описании теплопроводности металлов кроме решеточной составляющей, обусловленной фононами, необходимо учитывать и электронную составляющую.
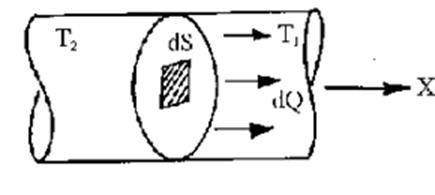
Рис. 2.2.10. К уравнению теплопроводности
При
рассмотрении теплопроводности часто исследуют не только величину коэффициента
теплопроводности l, но и обратную ему величину коэффициента
теплового сопротивления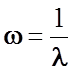 
, которая, подобно
l,
в трехмерном случае отражает анизотропию решетки и является тензором.
Причинами теплового сопротивления кристаллической решетки являются ангармоничность и затухание колебаний. При гармоническом законе тепловых колебаний каждая частица полностью отдавала бы свою энергию соседним частицам со скоростью звуковой волны, и коэффициент теплопроводности был бы бесконечно большим. Однако ангармоничность колебаний нарушает независимый характер нормальных колебаний решетки, происходит обмен энергией между частицами с отклонением от принципа суперпозиции, изменяется частотный спектр. Этот процесс удобно рассматривать в рамках фононной теории, представив себе кристалл в виде ящика, заполненного фононным газом. Причем фононы могут взаимодействовать друг с другом по законам, схожим с законами идеального газами, для них применимы такие понятия, как средняя длина свободного пробега lср, среднее число соударений в секунду zф, среднее время релаксации tф. Влияние ангармоничности колебаний проявляется в том, что фононы при взаимодействии могут сливаться или расщепляться. Такие процессы называются фононным рассеиванием. В металлах и полупроводниках на теплопроводность влияют не только фонон-фононные, но и электрон -фононные взаимодействия.
По предложению Дебая к фононам применимо соотношение теории идеального газа для коэффициента теплопроводности
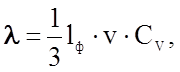(2.2.45)
где lф - средняя длина свободного пробега фононов в данной решетке при данной температуре, v - средняя скорость фононов, в первом приближении полагаемая равной скорости звука, Cv - удельная теплоемкость материала. В случае металлов и полупроводников предполагают, что коэффициент теплопроводности является результатом аддитивного сложения
l = lреш + lе, (2.2.46)
и
к величине lреш, описываемой формулой (2.2.45),
следует добавить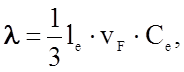 
где le - средняя длина свободного
пробега электрона (или "дырки" - в полупроводнике), vF - средняя скорость электрона,
соответствующая 
, Сe - теплоемкость электронного
газа.
Для определения точных значений l необходимо иметь точные данные о величинах, входящих в уравнения (2.2.45) и (2.2.46) и являющихся, в свою очередь, функциями большого числа параметров: температуры, структуры вещества, внешних воздействий, таких как электрические и магнитные поля, воздействие излучений, для пористых материалов - влажность и другие. Поэтому расчетным путем точное значение коэффициента теплопроводности установить практически невозможно, используются экспериментальные определения.
Полученные в большом количестве теоретические и эмпирические формулы для определения теплопроводности содержат или ряд серьезных упрощающих предположение, резко снижающих общность решений, или сложные теоретические функции, не допускающие получение точных решений в общем виде. Поэтому чаще всего они используются в исследовательской практике для интерпретации экспериментально полученных результатов и попыток качественного или полуколичественного предсказания теплопроводности материала в тех или иных условиях, если известны многие другие параметры вещества.
По причинам, изложенным выше, заранее предсказать величину теплопроводности реальных материалов в настоящее время теория не может. Однако практически очень важную температурную зависимость теплопроводности можно проанализировать с помощью уравнения (2.2.45). Качественно различные теоретические описания обычно используются при исследовании в областях температур Т <qД и Т > qД. Анализируется влияние различных факторов на величину lФ - среднюю длину свободного пробега фононов. Помимо рассеяния фононов на фононах, фононы в диэлектриках могут рассеиваться на других квазичастицах (магнонах, экситонах), точечных дефектах решетки (вакансиях и состоящих из них комплексах, примесных атомах), линейных дефектах (дислокациях), планарных дефектах (границах блоков в монокристаллах, очень сильно - на границах зерен в поликристаллах). Возможны и другие взаимодействия, например, с поверхностями, ограничивающими рассматриваемое тело.
Эти взаимодействия и определяют тепловое сопротивление решетки в области низких температур. Интегральная зависимость от температуры оказывается в этом интервале для подавляющего большинства веществ подобной зависимости теплоемкости СV:
l~T3D, (2.2.47)
где D - размер тела, например диаметр стержня, вдоль которого распространяется тепло.
У многих материалов в области 5K<T<100K отмечается наличие острого максимума теплопроводности (рис.2.2.11). Его происхождение связано с конкурирующим влиянием двух процессов: увеличением теплопроводности вследствие роста числа фононов при возрастании температуры и увеличением интенсивности фонон-фононного взаимодействия, снижающего теплопроводность. Конкретная величина максимума теплопроводности (около 6200 Вт/(м×К) у Al2O3) определяется также взаимодействием фононов с границами зерен и границами тела.
При температуре, приближающейся к дебаевской qД, фононная теплопроводность совершенных кристаллов достаточно точно описывается формулой Пайерлса:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.