Теплофизические свойства твердых тел, страница 10

2.2.8. Диффузия в твердых телах

Химические реакции в твердых фазах, перестройки решеток предполагают возможность перемещения в них атомов. В кристаллической решетке возможно несколько видов движений атомов:

1) колебание атомов около положений равновесия, причем амплитуда и энергия колебаний возрастают с температурой;

2) атом или ион, приобретший за счет тепловой флуктуации достаточную энергию, может перейти из своего регулярного места в узле решетки в междоузлие (Я.И.Френкель назвал этот процесс д и с с о ц и а ц и е й   связанных атомов);

3) диссоциированный атом или ион, после некоторого времени "жизни" в междоузлии, перескакивает в следующее междоузлие;

4) диссоциированный атом с определенной вероятностью занимает вакантный узел решетки (происходит, по Я.И.Френкелю, а с с о -ц и а ц и я  атомов);

5) вакантный узел решетки ("дырка", вакансия) заполняется атомом из одного из соседних узлов решетки, происходит миграция вакансии по объему решетки;

6) диссоциированный атом, находящийся в междоузлии, выталкивает атом из одного из соседних узлов, занимая его место, в результате наблюдается "эстафетный" механизм движения атомов.

Перечисленные здесь механизмы атомного движения в твердых телах описывают процесс диффузии - один из важнейших процессов переноса в твердых телах. Без знания закономерностей этого явления невозможно понять сущность таких процессов, как обжиг, легирование; именно диффузия определяет коррозию огнеупоров и металлов, спекание силикатных масс, газопроницаемость керамики, образование глазури и других защитных и декоративных покрытий на поверхностях.

Различают  с а м о д и ф ф у з и ю - перемещение атомов элементов в собственной кристаллической решетке и  г е т е р о д и ф ф у-

з и ю или атомную диффузию - перемещение атомов одного сорта в решетке из атомов другого сорта.

Теория процесса диффузии опирается на представления об обязательном существовании градиентов концентрации элементов.

2.2.8.1. Законы Фика

Подобно тому, как побудительной причиной теплопереноса является градиент температуры, первопричиной атомной диффузии является градиент концентрации вещества. В однофазном материале диффузия при постоянных значениях температуры и давления происходит таким образом, чтобы в результате переноса вещества градиент концентрации понижался. В случае одномерной диффузии первый закон Фика имеет вид

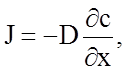                                                                          (2.2.53)

где  c - концентрация вещества; x - расстояние в направлениях диффузии;  - градиент концентрации; J - поток, количество вещества, проходящего за единицу времени через единицу площади, перпендикулярную направлению диффузии; D - коэффициент диффузии, обычно измеряемый в см²/с или м²/с.

Уравнение (2.2.53) по форме подобно уравнению Фурье для теплопроводности и закону Ома, утверждающему, что электрический ток пропорционален градиенту потенциала.

Разница потоков  входящего в данный элемент объема и выходящего из него, определяет изменение со временем концентрации в какой-либо точке вследствие явления диффузии.

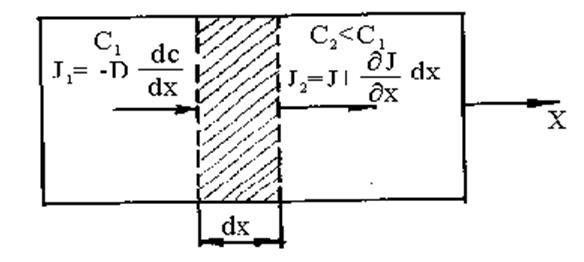        Рис.2.2.14. К выводу второго закона Фика

Если в объеме выделить две плоскости (рис.2.2.14), находящиеся на расстоянии dx друг от друга, то поток через левую плоскость будет равен

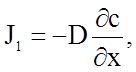
а поток через правую плоскость составит

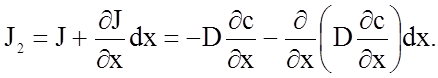                                (2.2.54)

После вычитания получим

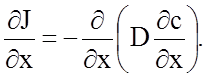                                                                 (2.2.55)

Изменение потока (J₁-J₂) определяет изменение концентрации в

выделенном сечении:

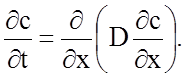                                                                  (2.2.56)

Уравнение (2.2.56) представляет собой второй закон Фика для одномерной диффузии, который, в случае независимости D  от концентрации, можно переписать в форме

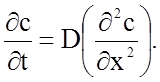                                                                      (2.2.57)

Решения уравнений второго закона Фика, при определенных для

конкретной физической задачи начальных и граничных условиях, обычно используются в практике экспериментальных исследований            процессов диффузии в твердых  телах. Из этих экспериментов и получают обычно информацию о таких параметрах диффузии, как  величина коэффициента диффузии в зависимости от температуры, концентрации примесей, дефектности структуры. Надежные данные о коэффициенте диффузии могут быть получены радиографическими методами или методом "меченых" атомов.

Например, на поверхность обычного никеля, состоящего из изотопов Ni⁵⁸ и Ni⁶⁰, можно электролитически осадить b-радиоактивный никель Ni⁶³. По почернению фотопластинки, вызванному бомбардировкой электронами, можно определить скорость самодиффузии никеля. Другие методы используют измерение энергетического спектра, в частности, a-частиц, испускаемых изотопом, диффундирующим в глубь образца. Последний метод позволяет обнаруживать перемещения атомов изотопа на 100...200Å  и измерять коэффициенты диффузии менее 10^-18 см²/с.

В последние годы многие результаты о параметрах диффузии получают средствами и методами элементного анализа, описанными в части 3. Наиболее интересны в практическом смысле два решения уравнения (2.2.57): для случая одномерной диффузии из постоянного источника и для одномерной диффузии из непостоянного источника.

2.2.8.1.1. Одномерная диффузия из постоянного источника

Пусть диффундирующее вещество, например серебро, поступает из обмазки в полубесконечное тело, например, в электротехническую керамику для создания электрического контакта. Координата плоскости поверхности тела X = 0, поверхностная концентрация С₀ поддерживается постоянной. Тогда, если t - время, граничные условия уравнения (2.2.57) выглядят следующим образом:

С(x,t) = C₀ при x = 0 и всех t,

C(x,t) = 0   при х > 0 и t =0 ,                                                 

C(x,t) = C  при x > 0 и t > 0.

Решение уравнения (2.2.57) выглядит так:

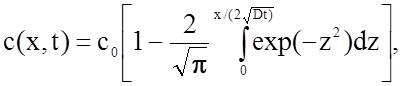                                   (2.2.58)