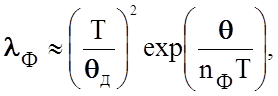(2.2.48)
где nФ - эмпирический коэффициент.
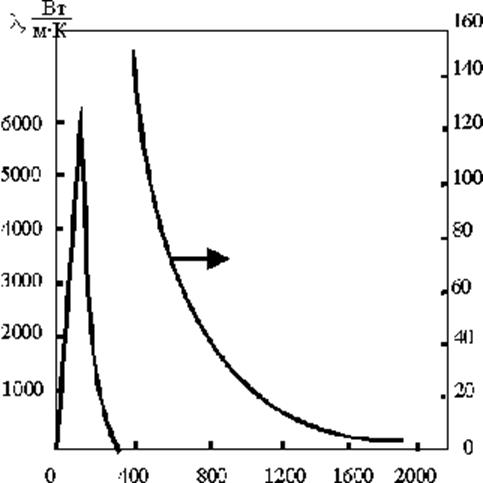
Рис.2.2.11. Теплопроводность Al2O3 в широком интервале температур.
Левая шкала относится к низкотемпературной области, правая - к высокотемпературной
Было также установлено, что при Т>qД
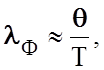(2.2.49)
т.е., поскольку теплоемкость вещества СV меняется уже мало и скорость распространения волн остается примерно постоянной, то определяющее влияние играет межфононное взаимодействие, при котором, вследствие высокой плотности фононного газа, средняя длина свободного пробега фононов lФ ~ 1/T очень мала по величине (lФ ~ 10-6 см), а у таких кристаллов, как TiO2, муллит, форстерит и других веществ с низкой теплопроводностью не превышает 2…4 Å, что соответствует межатомным расстояниям.
У огнеупорных окислов при Т> 1800К экспериментально обнаруживается некоторый рост коэффициента теплопроводности вследствие передачи некоторого количества тепла излучением. У прозрачных монокристаллов это явление отмечается и при более низких температурах.
Существенные изменения теплопроводности кристаллических материалов с изменением их химического состава, макро- и микроструктуры и проявление в различных интервалах температур разных механизмов теплопередачи требуют внимательного выбора табличных результатов, измерения этого параметра, приводимых в литературе, так как незначительные, на первый взгляд, изменения в стехиометрии и составе, влияние температуры - могут привести к существенным ошибкам в расчетах. Учитывая не слишком высокую в ряде случаев точность измерений, к справочным данным о величине коэффициента теплопроводности материалов следует относиться как к ориентировочным, требующим сравнений и дополнительной проверки в конкретных условиях использования.
Применение фононной теории к объяснению теплопроводности стекол и других материалов аморфного строения дополнительно осложнено нарушением дальнего порядка в расположении атомов. Однако в целом формула (2.2.45) все-таки остается применимой, хотя величины lФ, v и СV становятся еще более сложными для количественного вычисления; естественно лишь предположить, что lФ достигает порядка среднего межатомного расстояния.
В широком диапазоне не слишком высоких температур теплопроводность таких материалов, как кварцевое стекло, натрийкальцийсиликатные и боросиликатные стекла остается низкой и слабо зависящей от температуры вплоть до t » 600oС, выше которой заметный вклад начинает вносить перенос тепла излучением (эта доля становится пропорциональной Т 3 - рис.2.2.12).
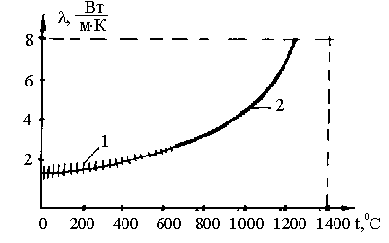
Рис.2.2.12. Теплопроводность кварцевого стекла, боросиликатного стекла и натрийкальцийсиликатного стекла. Область 1
При высоких температурах высокой теплопроводностью обладают фарфор и поликристаллическая керамика. Стекловидная силикатная фаза, присутствующая в керамике как связка, имеет теплопроводность, приблизительно равную теплопроводности стекол. Теплопроводность многофазной керамики зависит от распределения фаз и формы частиц и пор. Для определения многих параметров таких структур, в том числе теплопроводности, используют эмпирическую формулу
(2.2.50)
где n - показатель степени, лежащий в пределах между -1 и +1, vi - относительный объем, занимаемый фазой i.
Наинизшей теплопроводностью обладают
порошки тонко измельченных и плохо спекающихся материалов, таких как графит и
материалы с мелкими, сообщающимися между собой порами.
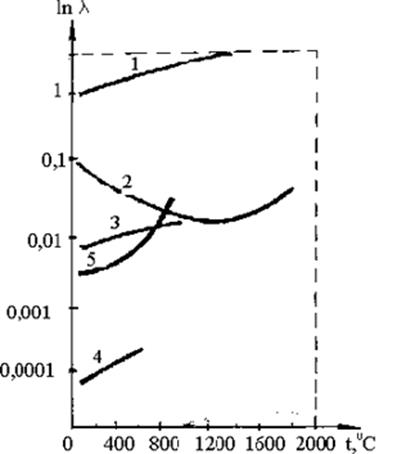
Рис.2.2.13. Теплопроводность (в логарифмическом масштабе) в зависимости от температуры: 1 - платина; 2 - чистая плотная MgO; 3 - шамотный огнеупор; 4 - порошок MgO; 5 - прозрачное кварцевое стекло
На рис. 2.2.13 представлены графики температурной зависимости теплопроводности чистой плотной MgO и порошка того же химического состава. Здесь же для сравнения приведены графики для широко распространенного теплоизоляционного материала шамота, типичного тугоплавкого металла - платины и прозрачного кварцевого стекла. Заметно различающиеся при комнатной температуре теплопроводности окиси магния, шамота и кварцевого стекла имеют близкую величину при повышенных температурах (800…1000oС).
При расчетах теплопередачи в случае установившегося теплового потока интегрируют уравнение (2.2.44), как это делается, например, для определения потерь тепла через стенки печи.
Если температура среды, через которую идет поток тепла, не остается постоянной, то скорость ее изменения со временем будет зависеть от теплопроводности среды, описываемой коэффициентом l, и ее теплоемкости, приходящейся на единицу массы rCp. В случае нестационарной задачи, т.е. определения теплопередачи при неустановившихся условиях, например, в процессе нагрева или охлаждения, а также при действии импульсных источников тепла, необходимо использовать величину температуропроводности
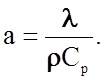(2.2.51)
Если считать величину коэффициента l не зависящей от температуры в рассматриваемом интервале и пренебречь зависимостью теплоемкости Ср от температуры, что вполне допустимо при Т>qД, то в
частном случае одномерного, вдоль оси Х распространения тепла быстрота повышения температуры в некоторой точке может быть найдена из дифференциального уравнения
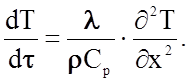(2.2.52)
Если уравнение (2.2.52)
представить в форме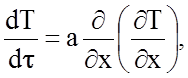 
то можно считать, что
коэффициент температуропроводности а, характеризует процесс установления
градиента температуры в направлении теплового потока. Поскольку процесс
распространения тепла очень существенно зависит от геометрических параметров -
формы нагреваемого или охлаждаемого тела, температуры и свойств окружающей
среды, то конкретные теплофизические задачи нагрева или охлаждения тел обычно
решаются численными методами. Конкретная задача сводится к известным
теоретическим решениям, приведенным в монографиях по теплопередаче, и решается
с использованием специальных таблиц (чаще всего функции erf
Гаусса), или номограмм, или с применением ЭВМ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.