Теплофизические свойства твердых тел, страница 3

Эта минимальная порция энергии тепловых колебаний решеток называется   ф о н о н о м. Кристалл, нагретый до некоторой температуры, можно представить в виде полости, заполненной квазичастицами -фононами ("фононным газом"), отражающими существование там поля упругих волн. Подобно другой квазичастице-фотону, фонон характеризуется  и квазиимпульсом

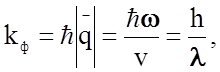                                                                 (2.2.15)

 - волновой вектор, v - скорость волны.

Аналогия фононов с фотонами может быть продолжена. Распределение фононов по энергиям подчиняется функции Бозе - Эйнштейна

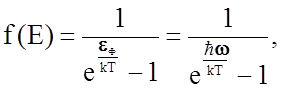                                                    (2.2.16)

а средняя энергия нормального колебания частотой w будет равна

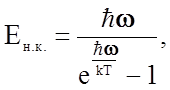                                                                    (2.2.17)

где k - постоянная Больцмана и Т - абсолютная температура. Последняя формула (2.2.17) учитывает, что функция f(Е) выражает среднее число фононов с энергией  .

Здесь уместно отметить, что кроме фононов, отражающих термическое возбуждение решетки и характеризующих упругое поле, для описания соответствующих возбуждений твердого тела применяются и другие квазичастицы:  п л а з м о н ы, как отражение коллективных электронных волн; м а г н о н ы  для представления спиновых волн перемагничивания; п о л я р о н ы, применяемые для описания локальной упругой деформации кристалла, связанной с движением электронов; э к с и т о н ы  - при описании волн поляризации.

Важнейшим тепловым параметром твердых тел является их  х а р а к т е р и с т и ч е с к а я   т е м п е р а т у р а   Д е б а я - температура, при которой в теле возбуждается весь спектр нормальных колебаний, включая и колебания с максимально возможной для данной решетки дебаевской частотой w_Д.

Ее можно определить, использовав величину энергии фонона дебаевской частоты, т.е.

откуда    

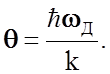                                                                               (2.2.18)

Температуры  принято считать  в ы с о к и м и. Дальнейшее (выше ) повышение температуры не изменяет частотного спектра кристалла, увеличивается лишь амплитуда колебаний атомов и, следовательно, средняя энергия колебаний, определяемая формулой (2.2.17).

Для многих веществ величина температуры Дебая  определяется чаще всего ультразвуковым методом.

2.2.4. Теплоемкость твердых диэлектриков

Под теплоемкостью тела понимают количество энергии, которое нужно затратить, чтобы повысить температуру тела на один градус. В качестве количественной меры в теоретических расчетах чаще всего используют молярную теплоемкость при постоянном объеме  С_V, причем

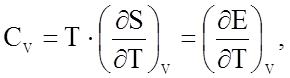                                                   (2.2.19)

где S  - энтропия, Е - внутренняя энергия, T - абсолютная температура. Экспериментально чаще определяют молярную теплоемкость  C_p (при постоянном давлении), причем величины  С_p и С_V для твердых тел различаются мало и этой разницей зачастую можно пренебречь.

Как свидетельствует эксперимент, теплоемкости кристаллов-диэлектриков, металлов и аморфных конденсатов различаются мало в широком интервале температур. При комнатной температуре величина теплоемкости почти всех твердых тел близка к 25 Дж/(моль×град) или около 6 кал/(моль×град) (эмпирический закон Дюлонга и Пти).

Кроме того, из экспериментальных данных известно, что с понижением температуры теплоемкость также понижается, в области абсолютного нуля стремясь к нулю по закону Т³ для диэлектриков и по закону Т¹ для металлов. Для сверхпроводников закон убывания может быть резче, чем Т¹.

2.2.4.1.Теории теплоемкости идеальных кристаллов по Эйнштейну и Дебаю

Известны несколько теорий теплоемкости. Но наиболее распространены две теоретических концепции теплоемкости кристаллических тел - Эйнштейна и Дебая. По Эйнштейну всякое кристаллическое тело представляет собой набор осцилляторов, имеющих одну и ту же резонансную частоту w, и колебание этих механических осцилляторов можно квантовать так же, как Планк квантовал осцилляторы излучения. Энергия системы из N линейных осцилляторов, имеющих одинаковую частоту, в соответствии с формулой (1.60) будет равна

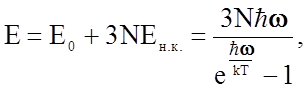                                                 (2.2.20)

где E₀ - "нулевая" энергия (при Т=0К), для одного моля она равна 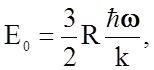 множитель 3 отражает наличие у каждого атома решетки трех степеней свободы, R – универсальная газовая постоянная. Теплоемкость С_V такой системы при N = N_A (число Авогадро) в соответствии с (2.2.19) будет равна

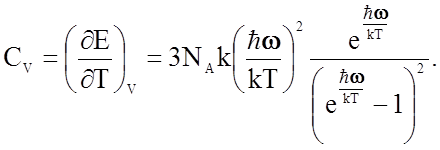                                  (2.2.21)

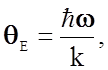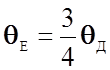В качестве предельного случая при высоких температурах формула (2.2.21) дает  С_V » 3N_Ak = 3R, что соответствует известному эмпирическому закону Дюлонга и Пти. В рамках модели Эйнштейна часто используют характеристическую температуру Эйнштейна,  которая связана с характеристической температурой Дебая  соотношением . Используя величину  и учитывая, что N_Ak = R, формулу (2.2.21) можно переписать в виде:

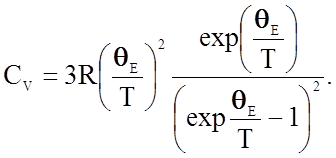                                             (2.2.22)

Теория Эйнштейна дает хорошее совпадение с экспериментом в области высоких температур, она до сих пор используется для аппроксимации оптической ветви фононного спектра.

В области низких температур эта теория предсказывает слишком быстрое убывание теплоемкости по экспоненциальной зависимости ~ , в то время как известно, что, по крайней мере для диэлектриков, закон убывания соответствует .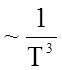

Для описания низкотемпературной акустической ветви фононного спектра шире применяется теория Дебая.

По концепции Дебая твердое тело, состоящее из N  одинаковых атомов, можно рассматривать как сплошную упругую среду, тепловое движение в которой сводится к акустическим колебаниям всевозможных частот (не превышающих w_Д), распространяющимся в виде упругих волн. Дебай сохранил основные положения теории Эйнштейна о гармонических осцилляторах, добавив предположение о возможности их колебаний с различными частотами.

Поскольку нормальные колебания распределены по частотам в соответствии с законом (2.2.10), на интервал частот  dw  будет приходиться энергия решетки

dE = E_н.к.×r(w)dw.                                                                  (2.2.23)