Теплофизические свойства твердых тел, страница 2

Рассматривая распространение упругих волн в трехмерной структуре, следует учитывать возможности движения атомов в трех взаимно перпендикулярных направлениях, что соответствует возбуждению и трех поляризованных упругих волн с разными в общем случае скоростями - продольной волны деформаций растяжения-сжатия и двух поперечных волн деформаций сдвига.

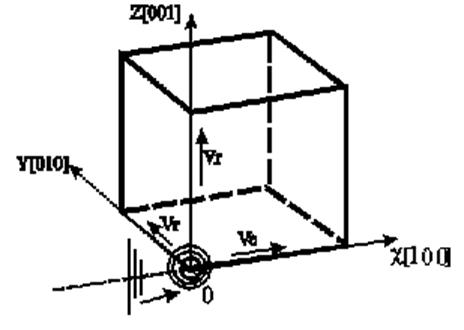В простой кубической решетке (рис.2.2.4) возбуждение атома, являющегося в узле [[000]] источником, действующим вдоль оси Х, приводит к возбуждению трех плоских волн, распространяющихся вдоль координатных осей - продольной волны, бегущей вдоль оси Х со скоростью v_l, и двух поперечных волн одинаковой амплитуды, распространяющихся также вдоль оси Х, но вызывающих смещение атомов в плоскостях, перпендикулярных оси Х, и соответствующим направлениям OY [010] и OZ [001]. В простой кубической структуре их скорости одинаковы, но меньше, чем у продольной волны (v_t<v_l), однако в кристаллах с меньшей симметрией скорости всех волн могут заметно  отличаться.  Причем, чем меньше  плотность вещества и выше  жесткость его межатомных связей, тем выше скорости распространения упругих (звуковых) волн.

Рис. 2.2.4. Возбуждения колебаний в кубической  решетке

Для точного теоретического определения величин v_l  и v_t используют соотношения теории упругости с применением понятий тензоров напряжений и деформаций и коэффициентов жесткости, представляющих набор упругих постоянных. Эти решения сравнительно просты лишь для высокосимметричных решеток.

2.2.2. Спектр нормальных колебаний, дебаевская частота

Уже из простейшей модели одномерной цепочки атомов видно, что возможно одновременное существование нескольких видов колебаний с различными частотами. Нормальные моды (виды) колебаний - это такие типы движений, при которых атомы колеблются с одной и той же частотой w по закону exp(-wt). Сильное взаимодействие атомов друг с другом в пространственной трехмерной решетке приводит к возможности одновременного действия множества осцилляторов. Анализ возможного набора частот колебаний атомов и является центральным вопросом в теории тепловых свойств твердых тел.

Сравнительно просто удается определить теоретически спектр частот совершенных решеток высокой симметрии - простая кубическая, ОЦК, ГЦК, гексагональная, и существенные сложности возникают при теоретических расчетах параметров многофазных и многокомпонентных структур. В этом случае данные спектрометрического эксперимента могут дать больше достоверной информации. Вместе с тем даже простейшие оценки представляют интерес.

Вернемся вновь к одномерной атомной цепочке длиной L (см. рис. 2.2.1). В такой цепочке могут возникнуть нормальные колебания, длины волн которых равны

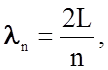          (n=1,2,3,….N),                                                (2.2.7)

где N - число атомов в цепочке, L - ее длина.

Чем меньше длина волны l_n колебаний (больше частота w_n), тем

труднее возбудить такие колебания. Число разных нормальных колебаний z  с длиной волны l, большей или равной l_n, очевидно, равно n:

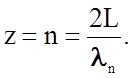
Тогда в трехмерном кристалле в виде куба с ребром L  и объемом  L³  наименьшее число колебаний с длинами l³l_n будет равно

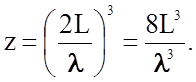
Более строгий расчет, учитывающий диагональные моды, дает

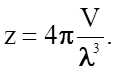
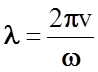Если учесть, что , то

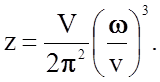                                                                         (2.2.8)

Распределение числа нормальных колебаний по частотам можно получить, продифференцировав уравнение (2.2.8)

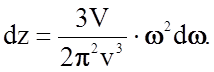                                                                 (2.2.9)

Формула (2.9) выражает число нормальных колебаний, заключенных в интервале от w до w + dw. Из формулы (2.9) можно выделить функцию   

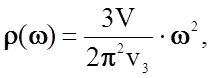                                                                (2.2.10)

определяющую  п л о т н о с т ь  заполнения спектрального участка dw нормальными колебаниями в окрестности w. Функция  r(w), определяющая частотный спектр колебаний, называется  ф у н к ц и е й   р а -с п р е д е л е н и я  нормальных колебаний по частотам. Так как в решетке с числом атомов N  общее число степеней свободы не превышает 3N, то функция r(w) должна удовлетворять условию нормировки 

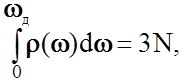                                                                  (2.2.11)

где w_д - максимальная частота нормальных колебаний в данной решетке.

Если в формулу (2.2.11) подставить функцию распределения (2.2.10) с фиксированным значением w = w_д , то после интегрирования получим

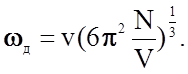                                                                     (2.2.12)

Частота w_д называется   х а р а к т е р и с т и ч е с к о й     д е б а- е в с к о й    ч а с т о т о й, ограничивающей спектр нормальных колебаний сверху. (Петер Йозеф Вильгельм Дебай - автор теории теплоемкости твердых тел, предложенной в 1912 году).

2.2.3. Понятие о фононах и других квазичастицах в твердом теле. Характеристическая температура Дебая

Энергия колебаний решеток является квантовой величиной. Для описания энергетических характеристик твердых тел введено понятие нормального осциллятора - такого физического объекта, энергия колебаний которого равна энергии нормального колебания решетки. Масса нормального осциллятора равна массе атомов, колеблющихся с частотой, равной частоте нормального колебания. Любой нормальный осциллятор представляет собой одно нормальное колебание решетки, в котором участвуют все атомы кристалла, его масса равна массе одного атома.

Полная энергия кристалла, состоящего из N атомов, совершающих связанные колебания, равна энергии 3N независимых нормальных гармонических осцилляторов. Как следует из решения уравнения Шредингера, где потенциальная энергия представлена в виде 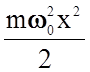 (m – масса осциллятора, w₀ - собственная круговая частота, x - смещение), энергия осциллятора квантована и определяется соотношением

E_n = (n + ½)            ( n = 0,1,2,3,..., )                           (2.2.13)

Энергетический спектр состоит из n равноотстоящих уровней

(рис.2.2.5), удаленных друг от друга на величину

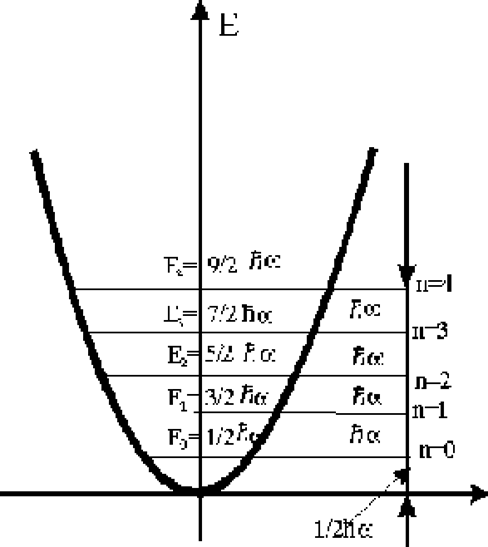
                                                            (2.2.14)

Рис.2.2.5. Энергия фононов в решетке