Математика \ Математическая статистика

Математична статистика в гірничо-геологічних розрахунках, страница 12

Перевірка: 74 = 122 + 2·(–44) + 40 – вірно.

З таблиці знаходимо умовні моменти:

М1 = -44/40 = –1,1; М2 = 122/40 = 3,05.

Вибіркова середня дорівнює:

 =М1·h +C = 380.

Вибіркова дисперсія дорівнює:

Dв = [M2 - (M1)2]·h2 = 73600

Вибіркове середнє квадратичне відхилення дорівнює

271,2932 .

S 2 =  ;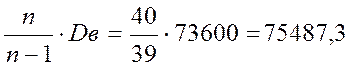

 .

Отримані результати дозволяють зробити наступні висновки.

Середній час безвідмовної роботи шляхового стопора по вибірці дорівнює 380 годин. Середній розкид часу безвідмовної роботи шляхового стопора навколо середньої по вибірці дорівнює 274,75 годин.

Перевіримо гіпотезу про показниковий закон розподілу ознаки Х. Використовуємо критерій Колмогорова-Смирнова.

Показниковий закон є однопараметричним розподілом з параметром l. Оцінимо параметр l за допомогою характеристик вибірки в такий спосіб:

l .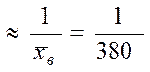

Для кожного інтервалу ознаки Х необхідно обчислити ймовірності потрапляння ознаки в даний інтервал. Використовуємо готову формулу з теорії ймовірності для величини, що має показниковий розподіл:

.

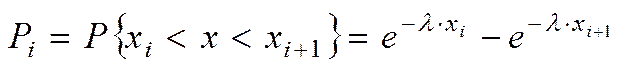Далі заповнимо таблицю, причому крайню ліву точку інтервалу заміняємо на 0 ; крайню праву точку заміняємо на + ¥, оскільки теоретичний показовий розподіл визначений для додатних значень аргументу.

Теоретичні частоти знайдемо за формулою:

 ,  n=40.

Знаходимо накопичені частоти (позначимо для емпіричних частот як n×Fn(x) ; для теоретичних частот – n×F(x)). Для цього треба для кожного інтервалу послідовно складаємо частоти, починаючи з першого інтервалу і закінчуючи поточним інтервалом. Потім обчислюємо модуль різниці накопичених частот у кожнім інтервалі ôn×Fn(x) – n×F(x)ô = n×ôFn(x) – ×F(x)ô. Заповнимо таблицю.

X i

X i+1

n i

Pi

n×Pi

n×Fn(x)

n×F(x)

ôn×Fn(x)–n×F(x)ô

100

300

24

0.55

21.84

24.00

21.84

2.16

300

500

6

0.19

7.43

30.00

29.27

0.73

500

700

4

0.11

4.39

34.00

33.66

0.34

700

900

3

0.06

2.59

37.00

36.25

0.75

900

1100

2

0.04

1.53

39.00

37.79

1.21

1100

1300

1

0.06

2.21

40.00

40.00

0.00

Сума

40

1.00

40.00

З останнього стовпця таблиці знаходять найбільше з отриманих модулів

n ×D = max{n×ôFn(x) – ×F(x)ô} = 2,16.

Визначаємо спостережуване значення критерію згоди Колмогорова – Смирнова

.

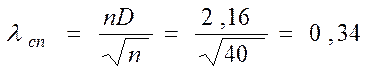Цей критерій є випадковою величиною, що підкоряється закону розподілу Колмогорова. За таблицею критичних точок (Додаток К), використовуючи заданий рівень значимості a = 0,2 , знаходимо критичне значення критерію

lкр = l(0,2) = 1,07.

Порівнюємо: lсп < lкр, виходить, що немає підстав відкинути нульову гіпотезу H0. Отже, гіпотезу про показниковий закон розподілу часу безвідмовної роботи стопора можна вважати правдоподібною.

5 Елементи кореляційного і регресійного
аналізу

Залежність між змінними випадковими величинами Х и У, при якій кожному значенню однієї з них відповідає визначене середнє значення іншої величини, називається кореляційною. Функція, що описує таку залежність, називається регресією. За типом функції розрізняють лінійну і нелінійну регресії, за кількістю залежних перемінних – одномірну і множинну регресії. Ознаку Х, що відповідає незалежній змінній, будемо називати факторною; ознаку У, що відповідає залежній змінній, будемо називати результативною.

5.1    Кореляційне поле

Нехай статистичні дані являють собою ряд пара зв'язаних значень числових ознак Х и У: (х1 ;y1), (х2 ;y2), ..., (хi ;yi), …, (хn ;yn) .

Кореляційне поле – це графічне представлення статистичних даних у прямокутній системі координат ХОУ, де кожній парі на площині відповідає точка. Побудоване кореляційне поле (рис. 5.1) дозволяє на початковому етапі дослідження зробити попередній висновок як про

наявність залежності між ознаками Х и У, так і про вид цієї залежності.

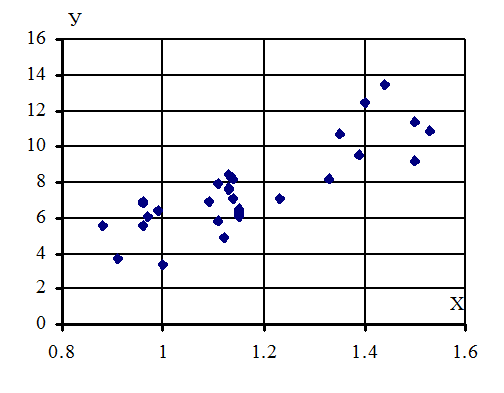
Рисунок 5.1

5.2    Емпірична ламана регресії

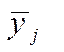Емпірична ламана регресії будується по точках, де хj – середини інтервалів розбивки ознаки Х; – середні групові значення ознаки У в кожнім інтервалі ознаки Х: 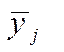= (Σ yi)/nj . Тут підсумовування ведеться тільки за тими значеннями yi , для яких значення хi потрапило в j-тий інтервал; nj – береться з інтервального статистичного ряду ознаки Х для j-го інтервалу.

5.3    Емпіричний коефіцієнт детермінації й емпіричне
кореляційне відношення

Для виміру тісноти зв'язку між ознаками Х и У застосовуються емпіричний коефіцієнт детермінації й емпіричне кореляційне відношення.

Емпіричний коефіцієнт детермінації знаходиться за формулою:

,

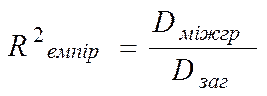де       Dміжгр – міжгрупова дисперсія результативної ознаки У;

Dзаг – загальна дисперсія результативної ознаки У (можна використовувати вибіркову дисперсію ознаки У, знайдену при одномірному аналізі).

Можна також дисперсії визначати за формулами:

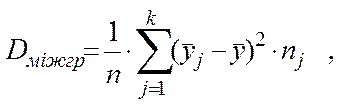                               (5.1)

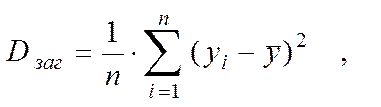                              (5.2)

де       k – число груп по факторній ознаці Х;

n – обсяг вибірки;

yi – індивідуальні значення результативної ознаки У;

 – його середні групові значення;

 – середнє значення ознаки У;

nj – частота в j – тій групі (береться зі статистичного ряду ознаки Х).

Емпіричне кореляційне відношення дорівнює кореню квадратному із коефіцієнта детермінації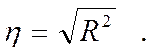

5.4 Лінійна регресія

а) Рівняння лінійної регресії з кутовим коефіцієнтом:

Рівняння лінійної регресії У на Х має вид:

,                                            (5.3)

де       k – коефіцієнт регресії;

b – вільний член рівняння регресії.

Параметри рівняння регресії визначаються за фактичними даними, що являють собою набір n пар (хi ;yi), за допомогою методу найменших квадратів (МНК).

Розрахункові формули мають вид:

,

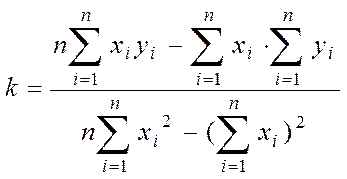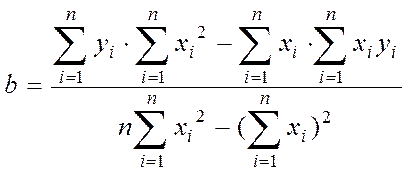.                         (5.4)

Скачать файл