Анализ приоритетных направлений развития транспортно-экспедиционной фирмы, страница 4

Pij = 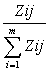,                                                          (2.2)

где Pij – оценка i–того фактора специалистом j в долях влияния причин на исследуемую величину.

Таблица 2.6 – Переход к долям влияния Pij

Операции перехода факторов к их оценке в долях влияния	Оценка важности факторов перевозочного процесса
	Стоимость перевозки	Комплексное обслуживание	Обеспечение сохранности	Выполнение срока доставки	Перевозка «от двери до двери»	Доставка к установленному времени
Эксперт 1	0,24	0,29	0,14	0,10	0,19	0,05
Эксперт 2	0,26	0,26	0,24	0,12	0	0,12
Эксперт 3	0,25	0,25	0,25	0,13	0	0,13
Эксперт 4	0,14	0,29	0,24	0,19	0,10	0,05
Эксперт 5	0,25	0,14	0,19	0,29	0,10	0,05
Эксперт 6	0,14	0,25	0,29	0,19	0,05	0,10
	1,28	1,48	1,35	1,02	0,44	0,5

В соответствии с полученными результатами экспертной оценки в качестве наиболее перспективного направления можно выделить фактор «комплексное обслуживание».Так же значимыми факторами экспертной оценки являются такие факторы, как «обеспечение сохранности» и «стоимость перевозки». Менее важными -«выполнение срока доставки», «доставка к установленному времени» и «перевозка «то двери до двери»».

2.3 Проверка согласованности экспертной оценки

Статистическую обработку оценок обычно начинают с проверки согласованности мнений специалистов.

Представляя оценки Pijкак значения результативного признака исследуемого процесса, изменение этого признака от строки к строке в итоговой таблице рассматривается как колебание его под воздействием некой обобщающей причины, колебания же по столбцам внутри одной строки – как наложение на оценку некоего случайного процесса, который характеризует разброс мнений экспертов, который не должен превышать какого-то предельного значения.

Таким образом, проверка существенности влияния причин на исследуемый процесс сформулирована в терминах факторного дисперсионного анализа. Характеристика степени влияния причин вычисляется по формуле

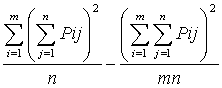= ,                                     (2.3) где n - число экспертов; m - количество рассатриваемых причин;тогда оценка некоего случайного процесса

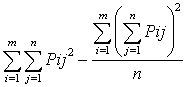=.                                          (2.4)

Далее, используя критерий Фишера, определяется значение функции распределения

F = .                                                      (2.5)

Тогда по формулам (2.3) – (2.5)

= ,

,

.

Чтобы найти табличное значение , величина вероятности ошибочного вывода принимается равной ю.Значение зависит от числа степеней свободы и .Принимаем, что  -степени свободы для большей дисперсии, - степени свободы для меньшей дисперсии. Тогда = n- (m+1)=6-(6+1)=-1, = m=6, где n- число экспертов; m- число анализируемых факторов.  принимается равным 1.Табличное значение = 5,99. Так как расчетное значение F (11,345,99), то с достоверностью не менее 95% можно утверждать, что влияние анализируемых факторов на исследуемый процесс является существенным, а оценки экспертов достаточно согласованными.

2.4 Вывод

В данной главе проведена обработка результатов экспертной оценки, в результате которой было определено, что в качестве наиболее перспективного направления  выделяется фактор «комплексное обслуживание».Так же значимыми факторами экспертной оценки являются такие факторы, как «обеспечение сохранности» и «стоимость перевозки». Менее важными  факторами - «выполнение срока доставки», «доставка к установленному времени» и «перевозка «то двери до двери»».