Методичні вказівки до лабораторних робiт з курсу «Теоретична і прикладна механiка», страница 5

Введемо позначення і визначимо множини

,

де  - постійні величини.

Задача 2.  (Прямий пошук у просторі відносних параметрів).

Знайти параметри  які  найбільшою мірою забезпечують виконання умов

 ,                                               (1.5)

                                              (1.6)

де   фіксовані значення відповідно кутів хитання і передачі. Мірою невиконання умов (1.5), (1.6) можуть правити функції             

Очевидно, якщо умова (1.5) виконується, то F₁=0. Додатні значення F₁  визначають міру невиконання умови (1.5). Аналогічний сенс має функція F₂ для умови (1.6). Тепер задачу 2 можна сформулювати так :

знайти 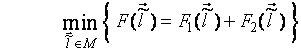                                   (1.7)

Для розв’язання задачі (1.7) використовується метод Бокса [4] і метод покоординатного спуску. Спочатку задача (1.7) розв’язується методом Бокса в автоматичному режимі з виведенням на екран інформації про мінімальне (F_min) значення функції цілі F. Це значення править орієнтиром при розв’язанні задачi методом покоординатного спуску у покроковому режимі з можливістю спостереження за процесом мінімізаціі на екрані. При зміні будь-якого з параметрів пошуку на екран виводяться поточні значення цих параметрів,  кутів хитання і передачі, а також значення функції F.

В процесі пошуку розв’язку задачі передбачена можливість регулювання кроку зміни параметрів, яку доцільно використовувати при підході до точки мінімуму функції шляхом зменшення  . Пошук припиняється якщо для заданого виконується умова