Методичні вказівки до лабораторних робiт з курсу «Теоретична і прикладна механiка», страница 10

w_1, w_2, w₃ -алгебраїчні величини кутових швидкостей ланок;        

Розв’язок системи (2.5), лінійної відносно w₂  і w₃ має вигляд

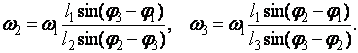                  (2.6)

Для визначення кутових прискорень      ланок треба продиференціювати за часом рівняння (2.5) і  знайти розв’язок системи двох рівнянь, лінійних відносно кутових прискорень e₂, e₃ . Опускаючи громiздкі проміжні викладки, наведемо тільки кінцевий результат   (при диференціюванні враховувалось, що dw₁/dt=0)

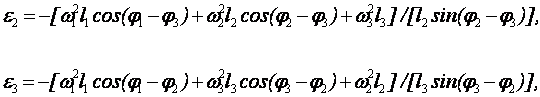      (2.7)

У співвідношеннях (2.6), (2.7) кути j_2, j₃  визначаються за формулами

                                       

де y  і g  знаходяться з (A.2)  i  (A.3).

Для визначення швидкості довільної точки Е, яка належить ланці ОА, АВ або ВD,  можна скористатися відповідно формулами

,

   або      

                               (2.8)                              

Проекції вектора прискорення точки Е визначаються як похідні за часом від проекцій вектора швидкості, тобто

де проекції  визначаються на підставі (2.8) з використанням формули (2.2). Зокрема, якщо точка Е належить ланці ВD, то вирази для  матимуть такий же вигляд, як і ліві частини рівнянь (2.5). Більш детально питання визначення швидкостей і прискорень точок, які належать ланці АВ, розглянуте у додатку Б.