Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 42

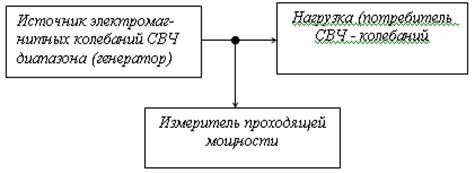
Рис. 17.8 Функциональная схема реализации метода измерения проходящей мощности СВЧ – колебаний

Под проходящей мощностью понимают разность мощностей падающей и отраженной электромагнитных волн.

В волноводных измерителях мощности разделение падающих и отраженных волн СВЧ – энергии производят волноводным направленным ответвителем.

Тема 8. Измерения параметров модулированных сигналов

Лекция 18. Измерения параметров модулированных сигналов

18.1. Измерение параметров амплитудно-модулированных сигналов.

18.2. Измерение параметров сигналов с угловой модуляцией.

18.1. Измерение параметров амплитудно-модулированных сигналов

Физический процесс управления параметрами (амплитудой, частотой и фазой) вспомогательного высокочастотного сигнала (несущего колебания) является модуляцией. При  скачкообразном (ступенчатом) управлении параметрами несущего колебания говорят об их манипуляции, что широко используется в дискретных системах передачи информации по радиоканалам.

С помощью несущего колебания, которое является в большинстве случаев гармоническим, осуществляют перенос спектр низкочастотного сигнала из источника сообщения в высокочастотный спектр передаваемого радиосигнала.

В общем случае модулированный сигнал можно представить в виде

или                            .

Основным методом измерения параметров модулированного сигнала является его наблюдение на экране осциллографа.

Математическую модель амплитудно-модулированного сигнала можно представить в виде

или   , где измеряемыми параметрами являются:

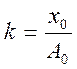- - коэффициент глубины амплитудной модуляции;

 - пределы изменения модулирующего сигнала;

А₀ – амплитуда несущего колебания;

х₀ = 1 – амплитуда модулирующего колебания;

ω₀ = const – частота несущего колебания;

φ₀ = const – начальная фаза колебания несущей.

На рис. 18.1 приведены осциллограммы измеряемого амплитудно-модулированного сигнала с разной глубиной модуляции.

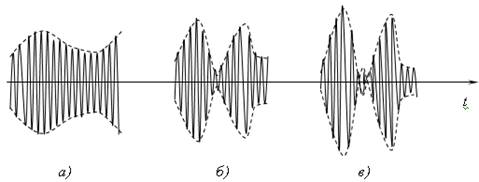
Рис. 18.1 Амплитудно-модулированные сигналы с неглубокой (а), с глубокой (б) и с перемодуляцией (в)

Из рассмотрения рис. 18, в следует, при перемодуляции, когда k> 1, происходит потеря повторения формы модулирующего сигнала.

В случае, когда модулирующим низкочастотным сигналом является гармоническое колебание с частотой Ω, то амплитудно-модулированный сигнал называется однотональным и его математическая модель имеет вид             

.  

Из этого выражения с учетом тригонометрической формулы произведения косинусов получаем

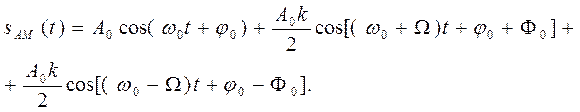   В этом выражении слагаемыми являются:

- несущая составляющая колебания;

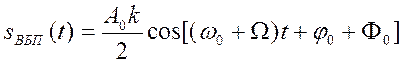
- составляющая верхней боковой полосы частотного спектра амплитудно-модулированного сигнала;

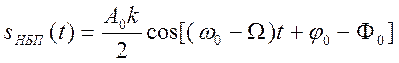
-  составляющая нижней боковой полосы частотного спектра амплитудно-модулированного сигнала.

Анализ 3-х последних выражений показывает на равенство амплитуд верхнего и нижнего боковых колебаний, а также на симметрию расположения этих спектральных составляющих относительно несущего колебания.

Средняя мощность амплитудно-модулированного колебания равна сумме двух слагаемых:

.         

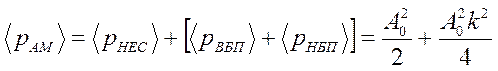Из этого выражения видно, что даже при 100% модуляции (k = 1) доля мощности обоих боковых колебаний составляет всего лишь 50% от мощности немодулированного несущего колебания. Поскольку информацию о сообщении несущая не несет, информация об этом сообщении заключена в боковых колебаниях, то можно отметить неэффективное использование мощности амплитудно-модулированного сигнала.

Поэтому на практике амплитудно-модулированные сигналы передают с помощью одной или двух одновременно боковых полос частотного спектра, подавляя несущую составляющую.

Поэтому измеряемыми параметрами амплитудно-модулированного сигнала являются мощность слагаемых боковых полос частотного спектра.