Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 31

Тема 5. Исследование формы и параметров сигнала

Лекция 13. Измерение параметров случайных сигналов

13.1. Измерение интегральной функции распределения.

13.2. Измерение плотности вероятности.

13.2. Определение корреляционных функций.

13.1. Измерение интегральной функции распределения

Интегральная функция распределения F(x) численно определяется как вероятность того, что все значения случайной величины Х(t₁) не превышают некоторого заданного уровня х:

F(x) = P[X(t₁) < x],                        

где Р – символ, характеризующий вероятность события.

Для случайной величины   Х(t₁), принимающей любые вещественные значения, интегральная функция распределения F(x) определяется на интервале

0 ≤ F(x) ≤ 1.                    

Принцип работы измерителя интегральной функции распределения основан на связи между функциями вероятностей и временем пребывания стационарного эргодического процесса в интервале заданных значений х.

Функциональная схема измерителя интегральной функции распределения случайного стационарного эргодического процесса и осциллограммы сигналов, поясняющие принцип его работы, приведены на рис. 13.1 и рис. 13.2 соответственно.

На рис. 13.1 и рис. 13.2 показано, что анализируемый случайный сигнал (реализация) u(t) через входное устройство, обеспечивающее необходимую интенсивность исследуемого процесса на входе основных блоков, подается на вход компаратора. Компаратор выполняет роль амплитудного селектора с определенным порогом срабатывания U₀, устанавливаемого источником регулируемого напряжения.

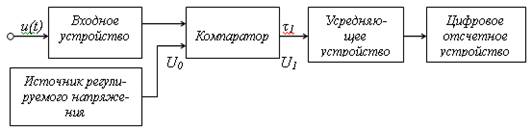
Рис. 13.1 Функциональная схема измерителя интегральной функции распределения случайного стационарного эргодического процесса

При срабатывании компаратора на его выходе возникает последовательность импульсов постоянной амплитуды  U₁  и случайной длительностью τ₁, которая в каждом случае пропорциональна времени пребывания анализируемой функции выше установленного значения напряжения  U₀.

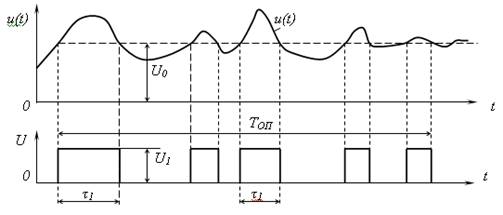
Рис. 13.2 Осциллограммы сигналов, поясняющие принцип работы измерителя интегральной функции распределения случайного стационарного эргодического процесса

Полученные таким образом импульсы поступают на вход усредняющего устройства, которое осуществляет усреднение за время измерения Т_ИЗМ, например, Т_ИЗМ = Т_ОП. Это усредняющее устройство может быть выполнено в виде интегратора или фильтра низких частот.

Выходное напряжение усредняющего устройства, отнесенное к амплитуде напряжения импульсов  U₁, соответствует математическому выражению 13.1, которое определяет характер изменения измеряемой интегральной функции распределения вероятности.

Таким образом на выходе усредняющего устройства получаем некую вспомогательную функцию

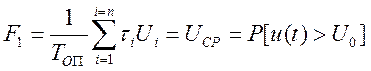,     с помощью которой можно дать оценку измеряемой интегральной функции распределения вероятности

F(u) = 1 – F₁ = 1 – P[u(t) > U₀] = P[u(t) < U₀].  

В качестве выходного цифрового отсчетного устройства применяют цифровые измерители временных интервалов, которые определяют сумму длительностей импульсов за время усреднения Т_ОП. Если произвести измерения интегральной функции распределения вероятности, меняя U₀, то получим график этой функции распределения.

Основная метрологическая погрешность измерения интегральной функции распределения вероятности определяется конечным временем усреднения, которое часто трудно задать обоснованно.

13.2. Измерение плотности вероятности

Если случайная величина Х(t₁) является непрерывной во времени, то часто вместо функции распределения удобнее пользоваться ее производной

,        

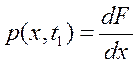называемой одномерной плотностью распределения вероятности.

Из этой формулы следует, что значение одномерной плотностью распределения вероятности

                          р(х, t₁)dx = F(b) – F(a) = P[a < X(t₁) < b],     

- есть вероятность попадания случайной величины Х(t₁)  в заданный интервал а, b.