Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 36

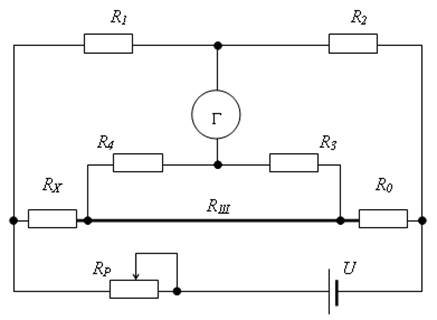
Рис. 15.2. Схема двойного моста постоянного тока для измерения малых, менее 1 Ома сопротивлений

На рис. 15.2 жирной линией обозначено сопротивлений шунта R_Ш. При равновесии двойного моста искомое измеряемое сопротивление найдем

.

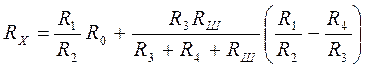Если соединительный провод, изображенный на рис. 15.2 жирной линией, выполнить из толстого медного провода, тогда R_Ш ≈ 0, и выражение (15.4) упрощается

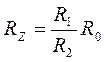, где R₀– образцовое сопротивление.

В режиме неуравновешенного моста измерение сопротивления производится по показаниям гальванометра, отградуированного в единицах сопротивления. Неуравновешенные мосты часто применяются в устройствах для разбраковки изделий по сопротивлению. Так, если при изготовлении резисторов необходимо отобрать из партии резисторы с сопротивлением  R = R_HOM ± ∆R, то уравновесив предварительно мост с помощью образцового магазина сопротивления при R_X = R_HOM, изменяют сопротивление магазина на ± ∆R  и фиксируют соответствие отклонения стрелки ± ∆α гальванометра с нулем посредине шкалы.  Затем, вместо магазина сопротивления ко входу моста подключаются контролируемые резисторы и если стрелка гальванометра выходит за допустимые пределы ± ∆α , резистор бракуется.

Чувствительность гальванометра S_Г представляет собой отношение

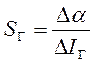, а чувствительность соединительной схемы S_CX моста определяется как

.              

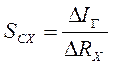С учетом выражений (15.6) и (15.7) получим формулу определения чувствительности всего моста

.  

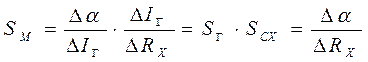Промышленностью выпускаются одинарные и одинарно-двойные мосты постоянного тока классов от 0,005 до 5.

Для измерения ёмкости, индуктивности и тангенса угла потерь конденсаторов применяются мосты переменного тока, рассмотрению которых уделим дальнейшее внимание.

15.2 Мосты переменного тока

Схема одинарного с четырьмя плечами моста переменного тока аналогична по начертанию схеме моста постоянного тока (рис. 15.1) и  представлена на рис. 15.3.

Плечи моста, изображенного на рис. 15.3, представляют собой комплексные сопротивления

Z= R + jX.

Равновесие моста переменного тока получим аналогично формуле

Z₁·Z₃ = Z₂·Z₄

Запишем последнее выражение в комплексной показательной форме

                                    _.

Рис. 15.3. Схема моста переменного тока

Из последнего уравнения найдем условия баланса моста переменного тока

Z₁·Z₃ = Z₂·Z₄

и                                      φ₁ + φ₃ = φ₂ + φ₄.                        

Анализируя последние выражения заключаем, что равновесие моста переменного тока наступает только при выполнении двух условий, а именно: при равенстве произведений модулей комплексных сопротивлений противоположных плеч и равенстве сумм их фазовых сдвигов.

Для измерения ёмкости конденсаторов без потерь используется мостовая схема, приведенная на рис. 15.4. Условие равновесия моста для этой схемы имеет вид

.

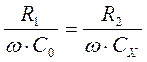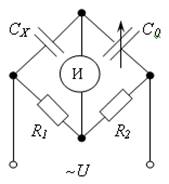
Рис. 15.4. Схема моста переменного тока для измерения ёмкости С_Х

Из этого выражения получим значение искомого измеряемого конденсатора

.

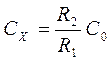Мостовая схема переменного тока для измерения индуктивности изображена на рис. 15.5

               Из рис. 15.5 следует, что в качестве плеча сравнения используется конденсатор переменной ёмкости С₀ . Полагая, что активное сопротивление катушки пренебрежимо мало (R_L = 0), получим условие равновесия

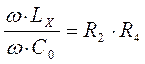, откуда находим искомое значение измеряемой индуктивности

.

Рис. 15.5. Схема моста переменного тока для измерения индуктивности L_X

С увеличением рабочей частоты метрологические погрешности измерения параметров электрических элементов  с помощью моста переменного тока растут.

15.3. Электронные измерители сопротивлений

Принцип построения функциональной схемы электронного омметра не отличается от принципа построения электронного вольтметра. Также используются передаточные свойства электронного усилителя и в электронных омметрах.

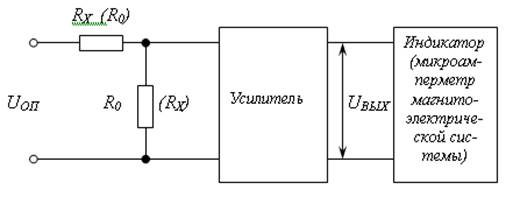
На рис. 15.6 изображена функциональная схема измерения с помощью  электронного омметра больших и малых сопротивлений, которая называется схемой стабилизированного тока.