Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 12

Для прямых однократных измерений с приближенным оцениванием погрешности в качестве результата измерения принимают значение отсчета х, а оценивание погрешностей производят грубо, а именно: на основе нормативных данных о свойствах используемых средств измерений. Такими нормами являются: пределы допускаемой основной погрешности прибора Δ_пр , дополнительные погрешности Ψ₁, Ψ₂ ,…, Ψ_т и др.

При однократных измерениях предел допускаемой абсолютной погрешности связан с классом точности γ_к.т. средства измерения формулой

,                                

где                                               -           

- стандартный ряд нормирующих значений верхнего предела измерения;

               α = 1,0; 1,2; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0; 7,5; 8,0 – коэффициент, значение которого подбирают в зависимости от измеряемой физической величины;

               п = 0; -1; -2; и т.д.

Класс точности приборов определен стандартным рядом чисел                                                                     ,  где п = 0; -1; -2; и т.д. имеет аналогичные значения как и для выражения .

Для электроизмерительных приборов классы точности 2,0; 5,0 и 6,0 исключены.

Верхняя оценка погрешности результата прямого однократного измерения Δ_∑ может быть найдена путем суммирования:

.             

После того как были оценены погрешности однократных прямых измерений перейдем к рассмотрению вопросов обработки результатов косвенных измерений.

5.2. Обработка косвенных измерений

При косвенных измерениях искомое значение физической величины А находят расчетом измеренных других величин а₁,…, а_т, связанных с измеряемой величиной А известной зависимостью

                                             А = f(a₁, a₂, … , a_m).    

Для оценки погрешностей имеет важное значение разделение косвенных измерений на линейные и нелинейные.

При линейных косвенных измерениях уравнение измерения имеет вид

,        

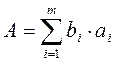где  b_i – постоянные коэффициенты при аргументах а_i.

Погрешности измерения аргументов могут быть заданы как своими допустимыми границами Δа_i, так и доверительными границами Δа(Р)_iс доверительными вероятностями Р_i.            

Полагая, что в заданных допусковых границах погрешности аргументов а_i

распределены равномерно, то доверительные границы Δа(Р) погрешности косвенного измерения рассчитываются по формуле

,             

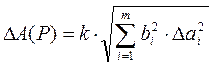где k – коэффициент, определяемый принятой доверительной вероятностью, например, при Р = 0,95 имеем k = 1,1. 

Если погрешности измерения аргументов заданы доверительными границами с одинаковыми доверительными вероятностями, то полагая распределение этих погрешностей нормальным, доверительные границы результата находят с помощью формулы

.                 

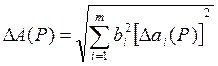Отметим, что любые другие функциональные зависимости (5.8) относятся к нелинейным косвенным измерениям.

Для нелинейных косвенных измерений применяют приближенные методы оценки погрешностей, основанные на линеаризации функциональной зависимости .

.          

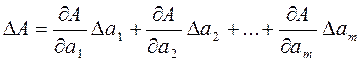В выражении предполагается, что погрешности измерения аргументов а_i  всегда являются малыми величинами по сравнению с номинальными значениями аргументов и дифференциал функции (А = f(a₁, a₂, … , a_m)). есть погрешность результата измерения ΔА .

Полагая, что распределения погрешностей аргументов а_i  подчиняются равномерному закону, при числе слагаемых т < 5 границы погрешности результата можно определить по формуле

                                               ΔА = Δа₁+ Δа₂ +…+ Δа_т .                  

Если принять закон распределения погрешностей аргументов а_i  нормальным, то оценку погрешностей косвенных измерений следует вычислять по (5.11), где коэффициенты b_i выполняют роль частных производных  в выражении ().

Из анализа выражения () следуют следующие правила оценивания погрешности результата косвенного измерения.

1. Если А = а₁ ± а₂ , то ΔА = Δа₁ + Δа₂.

2. Если  А = а₁·а₂, то δа₁ + δа₂ или, если 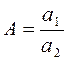, то .

3. Если А = В·а, где В не имеет погрешности, то δА = |B|δa.