Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 11

- среднеквадратичное отклонение при нормальном распределении случайной погрешности;

- математическое ожидание случайной величины при ее нормальном законе распределения;

- среднеквадратичное отклонение при равномерном распределении случайной погрешности в интервале от х₁ до х₂;

При нормальном распределении погрешностей принято считать случайную погрешность с границами ±3σ предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируются как грубые или промахи.

Для единообразия в оценивании случайных погрешностей интервальными оценками доверительная вероятность принимается равной 0,95.

В случае некоррелированных случайных погрешностей математические выражения среднеквадратичных отклонений () и () вычисляются путем их суммирования

.

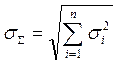Полученные математические выражения справедливы только при условии бесконечно большого числа опытов. В реальных условиях число измерений ограничено. Правила обработки измерительных данных с ограниченным числом измерений рассмотрено в следующей лекции.

Тема 2. Погрешности измерений

Лекция 5. Обработка результатов измерений

5.1. Обработка результатов прямых однократных измерений.

5.2. Обработка косвенных измерений.

5.3. Обработка результатов многократных измерений.

5.1. Обработка результатов прямых однократных измерений

Подавляющее большинство технических измерений являются однократными, особенностью которых является то, что законы распределения случайных погрешностей неизвестны и представление о них приходится формировать на основе ограниченной априорной информации.

Однократный отчет х включает в себя инструментальную, методическую и личную составляющие погрешности измерения, в каждой их которых могут быть выделены систематические и случайные составляющие.

Инструментальная систематическая погрешность выявляется путем поверки или по паспортным данным прибора. При анализе метода измерения можно оценить систематическую погрешность методического происхождения. Личная систематическая погрешность принимается пренебрежимо малой величиной.

Обработка результатов прямых однократных измерений возможна как с точным оцениванием погрешности, так и с приближенным.

При точном оценивании прямых однократных измерений после исключения из отсчета всех известных систематических погрешностей можно полагать, что погрешность исправленного результата х_испр состоит из неисключенных остатков систематических и случайных составляющих погрешностей.

Неисключенные систематические погрешности переводят в разряд случайных. Если заданы границы θ_i случайных погрешностей, то предполагается, что закон распределения вероятностей является равномерным, а если заданы значения средне квадратичных отклонений, то закон распределения вероятностей принимается нормальным.

В качестве границ случайных неисключенных систематических погрешностей принимают пределы допустимых погрешностей образцового измерительного средства, которое использовалось при поверке.

Средне квадратичные отклонения σ_i случайных погрешностей предварительно находятся опытным путем по результатам многократных наблюдений, либо доверительными границами Δх.

Доверительные границы ε результирующей случайной погрешности определяются по формулам

,

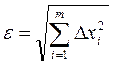, где  т – количество неисключенных систематических составляющих погрешности;

t – коэффициент Стьюдента, который будет рассмотрен ниже;

Получив по отдельности оценки неисключенной систематической и случайной погрешностей результата однократного измерения, необходимо сопоставить их между собой.

Во избежание появления чрезмерно грубой погрешности однократное измерение рекомендуется повторить 2 – 3 раза, приняв за результат среднее арифметическое. Статистической обработке эти отсчеты не подвергаются. Результат однократного измерения записывается в форме

                                                х_испр±Δ,    где Δ – предел допускаемой абсолютной погрешности.