Как следует из рис. 9.2 гармонический сигнал u1, период ТХ которого требуется измерить, после прохождения входного устройства и формирователя импульсов 1 преобразуется в последовательность коротких импульсов u2 c аналогичным периодом. В устройстве формирования и управления из них формируется строб-импульс u3 прямоугольной формы и длительностью ТХ, поступающий на один из входов временного селектора. На второй вход этого селектора подаются короткие импульсы u4 с образцовым периодом следования Т0, созданные формирователем 2 из колебаний генератора опорной (образцовой) частоты.
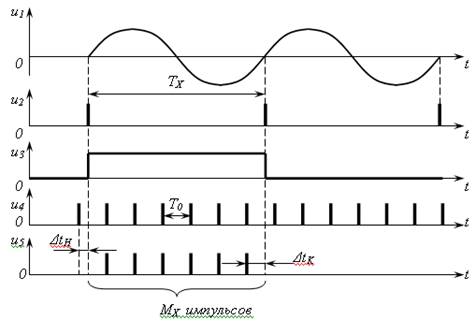
Рис. 9.2 Временные диаграммы, поясняющие метод цифрового измерения интервалов времени
Временной селектор пропускает на вход счетчика МХ счетных импульсов u4 в течение времени ТХ, равном длительности строб-импульса u3.
Измеряемый интервал ТХ, как следует из рис. 9.2, имеет значение
ТХ = МХ∙Т0 + ΔtД,
где ΔtД = ΔtH - ΔtK – общая погрешность дискретизации;
ΔtH иΔtK – погрешности дискретизации начала и конца измеряемого интервала времени ТХ..
Число импульсов, поступивших на вход счетчика, при ΔtД ≈ 0 в формуле (ТХ = МХ∙Т0 + ΔtД) равно
![]() .
.
Из этого выражения получаем искомое значение измеряемого интервала времени
ТХ = МХ ∙Т0.
Выходной код счетчика, выдаваемый на вход цифрового отсчетного устройства, соответствует числу подсчитанных им счетных импульсов МХ, а показания цифрового отсчетного устройства – измеряемому периоду ТХ, поскольку период следования счетных импульсов u5 выбирается из соотношения
Т0 = 10-п,
где п – целое число.
Так, например, при п = 6 в формуле (Т0 = 10-п), то цифровое отсчетное устройство отображает число МХ, соответствующее измеряемому периоду ТХ , выраженному в мкс.
Погрешности цифрового измерения интервала времени, как и цифрового измерения частоты, имеют систематическую и случайную составляющие.
Систематическая составляющая зависит от стабильности δКВ образцовой частоты кварцевого генератора, а случайная составляющая погрешности цифрового измерения интервала времени определяются погрешностью дискретизации (ТХ = МХ∙Т0 + ΔtД,) ΔtД.
Суммарная относительная погрешность цифрового измерения интервала времени определяется аналогично выражению (9.2) в процентах по формуле
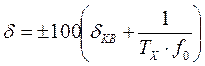 .
.
Из этой формулы следует, что точность измерения можно повысить за счет увеличения частоты f0 генератора образцовой частоты, например, путем умножения частоты его кварцевого генератора в К – раз, то есть за счет увеличения числа счетных импульсов МХ. С этой целью в схему (рис. 9.1) после входного устройства вводят делитель частоты исследуемого сигнала с коэффициентом деления К (на рис. 9.1 он не показан). При этом измеряется К периодов ТХ и в К раз уменьшается относительная погрешность.
Погрешность дискретизации можно уменьшить путем измерений с многократными наблюдениями, что нежелательно увеличивает время измерения.
Существует интерполяционный способ уменьшения погрешности дискретизации с небольшим увеличением времени цифрового измерения интервала времени.
Сущность интерполяционного способа уменьшения погрешности дискретизации состоит в том, что помимо целого числа периодов счетных импульсов, заполняющих измеряемый интервал времени, учитываются и дробные части периода, заключенные между последним счетным импульсом и интервальным.
9.3. Цифровые фазометры
В гармоническом колебании u1(t) = Umsin (ωt + φ1) величина φ1 называется начальной фазой.
Фазовым сдвигом Δφ двух гармонических сигналов одинаковой частоты u1(t) = Umsin (ωt + φ1) и u2(t) = Umsin (ωt + φ2) является модуль разности их начальных фаз:
Δφ = | φ1 - φ2|.
Величина Δφ = φ1 - φ2 называется разностью фаз.
Для измерения фазового сдвига используются фазометры. В качестве регулируемого и нерегулируемого средства сдвига фазы применяют фазовращатель, то есть четырехполюсник, у которого выходной сигнал задержан по фазе относительного входного.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.