Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 32

Если параметр а → ∞, а bпринимает текущее значение переменной х, тогда ранее измеренная интегральная функция распределения (13.1) выражается через плотность распределения следующим образом

.  

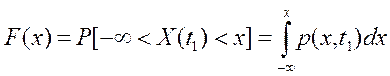Отметим, что одномерная плотность распределения вероятности является неотрицательной величиной и площадь кривой р(х, t₁) равна единице.

Плотность распределения вероятности анализируют с помощью устройства, функциональная схема которого приведена на рис. 13.3.

Из рис. 13.3 видно, что устройство для измеренияплотности вероятности содержит два канала измерения, подобных ранее рассмотренному устройству для измерения интегральной функции распределения вероятности. В каналах устанавливают уровни селекции по напряжению U₀ и U₀ + ΔU .

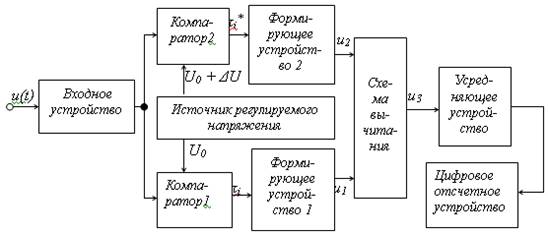
Рис. 13.3 Функциональная схема для измеренияплотности вероятности

Временные диаграммы, поясняющие принцип определения одномерной плотности вероятности случайного процесса с помощью временных интервалов, представлены на рис. 13.4.

На выходе компаратора 1 формируются импульсы напряжения u₁, длительность которых τ_i соответствует интервалам времени, когда

u(t) > U₀.     

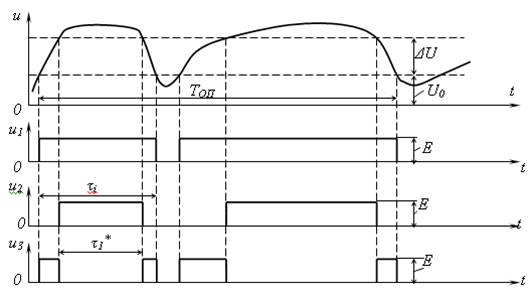
Рис. 13.4 Временные диаграммы, поясняющие принцип определения одномерной плотности вероятности случайного процесса с помощью временных интервалов

Для компаратора 2 длительность τ₁^* импульсов u₂  соответствует интервалам времени, когда

u(t) > U₀ + ΔU.

Далее импульсы напряжения обоих каналов поступают на входы соответствующих формирующих устройств 1 и 2.

Схема вычитания предназначена для вырабатывания разностного напряжения каналов:

u₃ = u₁ – u₂.

Длительность импульсов напряжения u₃ на выходе схемы вычитания соответствует интервалам времени, когда

U₀ <  u(t) < (U₀ + ΔU).

Усреднение этих импульсов за время накопления определяет величину, соответствующую оценке плотности вероятности случайного процесса при конечном времени усреднения Т_ОП. Меняя пороговый уровень   U₀, можно получить искомую зависимость р(и).

В соответствии с определением плотности вероятности для интервала наблюдения Т_ОП имеем

,

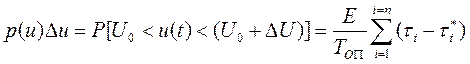Где         ;    .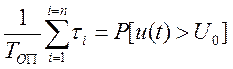

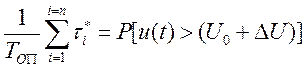Основная метрологическая погрешность измерения плотности распределения вероятности определяется конечным временем усреднения Т_ОП.

13.3. Определение корреляционных функций

Для исследования скорости изменения во времени и длительности случайных сигналов используют корреляционные характеристики. Приборы, измеряющие значения функции корреляции, называют коррелометрами.

Количественная оценка степени отличия (связи) исходного сигнала (оригинала) и(t) и его смещенной во времени копии u(t + τ) осуществляется с помощью автокорреляционной (корреляционной) функции.

Если сигнал детерминированный с конечной длительностью, то автокорреляционная функция записывается

.    

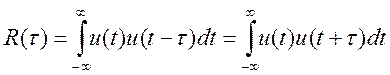Автокорреляционная функция (13.9) обладает свойством четности:

R(τ) = R(-τ). 

В теоретических расчетах частот используют нормированную автокорреляционную функцию

,     

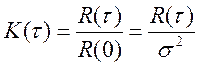где R(0) = σ².

Для случайных стационарных эргодических процессов с интервалом наблюдения Т_ОП корреляционную функцию отображают формулой

.                     

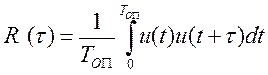В электрорадиоизмерениях вводят удобный для анализа степени связи (корреляции) сигнала и его копии, или для анализа связи разных сигналов числовой параметр – интервал корреляции, который равен ширине основания автокорреляционной функции.

При исследовании связи между двумя случайными сигналами х₁(t) и  х₂(t)   используют взаимокорреляционную функцию, которая в случае их эргодичности имеет вид

.     

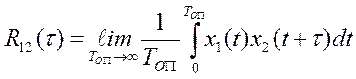В метрологии целью корреляционного анализа является численная оценка функции корреляции для различных временных задержек τ. Эти оценки можно находить последовательно во времени (последовательным коррелометром), когда время задержки τ последовательно меняется, или одновременно (параллельно) с помощью многоканального коррелометра при фиксированной задержке τ.

Последовательный корреляционный анализ применяют при исследовании стационарных случайных процессов, статистические характеристики которых не зависят от начала отсчета времени.