Преимущество вычисления модуля гармонической слагаемой с помощью предлагаемой формулы по сравнению с известной методикой нахождения тригонометрической интерполяции очевидно. Алгебраически складываются порознь четные и нечетные составляющие ступенек уi и полученные результаты лишь возводятся порознь в квадраты.
Фазовый сдвиг модулей гармонических составляющих определяется с помощью формулы
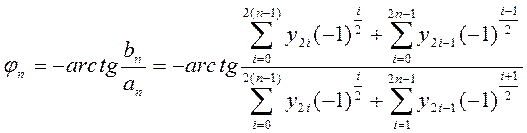 .
.
Получим искомое продолжение математической зависимости для нахождения сдвига фаз гармонических составляющих Фурье φп
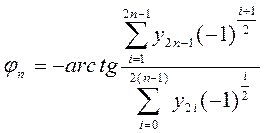 .
.
Полученная математическая зависимость обеспечивает наиболее простой прием вычисления сдвига фаз гармонических составляющих Фурье.
Тема 5. Исследование формы и параметров сигнала
Лекция 12. Нелинейные искажения и случайные процессы
12.1. Измерения нелинейных искажений.
12.2. Измерение математического ожидания случайного процесса.
12.3. Измерение дисперсии случайного процесса.
12.1 Измерения нелинейных искажений
Нелинейные искажения возникают в цепях с нелинейной амплитудной характеристикой. При прохождении по таким цепям с нелинейной амплитудной характеристикой колебаний происходит искажение их гармонической формы и в спектре появляются высшие гармоники.
Возникающие при нелинейных искажениях гармоники можно исследовать и измерить с помощью анализаторов спектра.
Наиболее распространенным показателем нелинейных искажений является коэффициент нелинейных искажений (коэффициент гармоник), представляющий собой отношение действующего значения высших гармоник U2, U3, … , Un напряжения (или тока) к действующему значению его первой гармоники U1:
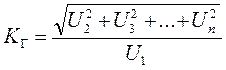 .
.
Для измерения относительного значения напряжения гармоник можно использовать анализатор спектра, если его разрешающая способность позволяет наблюдать раздельно спектральные составляющие. Если детектор анализатора линейный, то в формулу вместо напряжений U1, U2, … , Un можно подставить значения их амплитуд, измеренных на экране (рис. 11.3) анализатора в единицах длины.
Существуют специальные измерители нелинейных искажений, функциональная схема аналого-цифрового типа которых приведена на рис. 12.1.

Рис. 12.1 Функциональная схема аналого-цифрового измерителя нелинейных искажений
Принцип работы аналого-цифрового измерителя нелинейных искажений основан на подавлении с помощью заграждающего фильтра основной частоты.
Входное устройство служит для согласования измерительного прибора с источником исследуемого сигнала.
Перед измерением переключатель Кл ставят в положение Калибровка, с помощью усилителя уровень исследуемого напряжения повышают до такого фиксированного значения, при котором электронный цифровой вольтметр действующего значения будет проградуирован в величинах коэффициента нелинейных искажений. При этом измеряется действующее значение напряжения всего исследуемого сигнала (всех гармоник)
![]() .
.
Затем переключатель Кл прибора ставят в положение Измерение. Настраивая заграждающий фильтр, подавляют напряжение основной частоты (первой гармоники U1 ). Цифровой вольтметр показывает минимальное значение, которое соответствует действующему (эффективному) значению суммы высших гармонических составляющих сигнала:
![]() .
.
Сравнивая показания во втором и первом случае, определяют коэффициент искажений
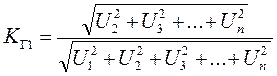 .
.
Из этого выражения определяют искомый коэффициент нелинейных искажений
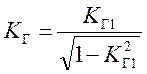 .
.
При небольших нелинейных искажениях результат вычисления коэффициента гармоник с помощью 2-х последних формул будет отличаться не более 1%.
Обычно измерители нелинейных искажений применяют для измерения коэффициента гармоник КГ в пределах 0,1 – 30 %, в диапазоне частот от 0,01 кГц до 10 МГц.
12.2. Измерение математического ожидания случайного процесса
К числовым характеристика случайного процесса относятся математическое ожидание и дисперсия.
Математическое ожидание (среднее) случайного процесса х в метрологии имеет значение истинной величины и вычисляется аналоговыми приборами по формуле
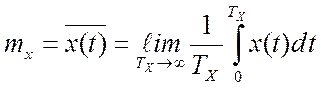 ,
,
где ТХ – интервал наблюдения случайного процесса х.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.