Основы метрологического обеспечения. Краткий исторический обзор развития метрологии. Нормативные документы, регламентирующие метрологическое обеспечение, страница 28

Недостатком цифрового спектрального анализа с помощью дискретного преобразования Фурье () является большое время вычислений, так как требуется примерно выполнить

N∙ℓog₂N

операций умножения.

Быстрое преобразование Фурье позволяет многократно сократить число вычислительных операций умножения и основано на прореживании во времени (децимации – от греч. слова деци – доля) заданной последовательности отсчетов дискретного сигнала на ряд промежуточных последовательностей, в каждой из которых можно заменить сложные операции умножения на более простые операции алгебраического сложения комплексных чисел.

Для этого исходную последовательность четных N отсчетов представляют в виде двух подпоследовательностей с четными и нечетными номерами и, кроме того, анализируют только половину чисел каждой подпоследовательности с помощью соответствующих  формул

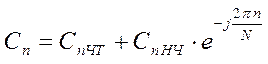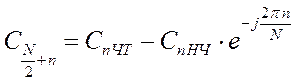 при п = 0, 1, 2, … , ,         при п = 0, 1, 2, … , .        

Далее чтобы уменьшить число вычислений каждую подпоследовательность еще раз также разбивают на две промежуточные части.

Разбиение и уменьшение в два раза число членов подпоследовательностей выполняют N² раз до тех пор, пока их останется четыре. Четырехэлементные последовательности отсчетов легко позволяют проанализировать спектр сигнала.

Выигрыш уменьшения вычислительных операций за счет быстрого преобразования Фурье в сравнении с формулой (N∙ℓog₂N) составляет

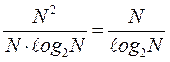 раз.

Современные цифровые анализаторы обладают широкими функциональными возможностями и позволяют:

- восстанавливать сигнал по его спектру;

- анализировать и синтезировать характеристики электрических цепей, а именно: определять передаточные функции, временные (импульсные, переходные) и частотные (амплитудные, фазовые) характеристики, устойчивость и запасы структурной устойчивости;

- выполнять цифровую обработку и фильтрацию сигналов (перемножение спектров, операция свертки);

- спектральный анализ периодических, импульсных и случайных сигналов, а именно: определение модуля, фазового сдвига и комплексных составляющих спектра;

- измерение параметров аналоговых (амплитуды, частоты, фазы, индекса модуляции, девиации и разноса частоты) и дискретных (амплитуды, длительностей импульса, его подъема и спада, периода следования) сигналов;

- корреляционный анализ как детерминированных, так и случайных сигналов;

- анализ статистических характеристик случайных процессов.

Не ухудшая точность спектрального анализа известными цифровыми методами предлагается новый способ численного гармонического анализа, названный по имени его автора.

11.4 Способ анализа спектра сигналов Краснова Е.А.

Предлагается [3] представить анализируемую функцию у(t)  в виде совокупности четных ступенек у_i при i = 0, 1, 2, … , 2n, где  n - порядковый номер гармоник Фурье.

В результате числового гармонического анализа, при котором квантование исследуемой функции заменяется четным значением ступенек, имеем:

.

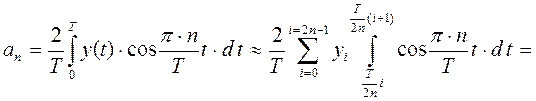
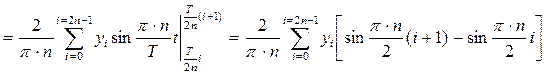Выражение запишем в виде суммы четных и нечетных слагаемых

.    

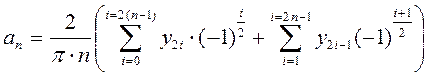Аналогично методике вывода формул найдем математическое выражение для вычисления синусоидальной гармонической составляющей Фурье:

.   

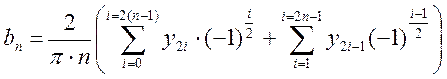С учетом полученных формул искомая амплитуда (модуль) гармонической составляющей определяется с помощью выражения ():

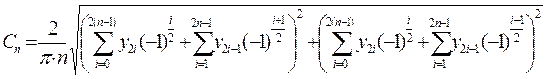
Последовательно анализируя полученное выражение при п = 1, 2, 3, 4, …  можно выявить следующую зависимость:

;                                                                               

;                                                           

;                                            

;                           

.     .     .     .     .     .     .     .     .     .     .     .     .     .     .     .     .

.

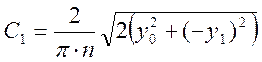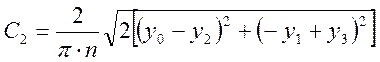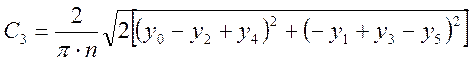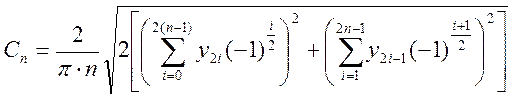Сравнивая формулы заключаем, что процедура вычисления модулей гармонических составляющих Фурье анализируемого сигнала у(t) существенно упрощается.