Засоби технологічного оснащення. Технологічне обладнання. Технологічна оснастка. Пристосування. Інструмент. Верстатні пристосування, страница 17

 , де  r  - радіус цапфи ексцентрика, мм;  ∆ - товщина перемички, мм.

Величини    e і  ρ  визначають з рівності

, де f – коефіцієнт тертя спокою у цапфі; при ;   f=0,12...0,5 для полусухих поверхонь або  при f=0,1

Кут повороту ексцентрика при затиску деталі

Ширину робочої частини ексцентрика знаходять по допустимим напругам, по модулям пружності і коефіцієнтам для матеріалу ексцентрика і елементам, які контактують з ним

; 

W – сила затиску деталі, Н(кгс)

Е – модуль пружності,

σ - допустима напруга на зімнення, σ=60

Всі отримані дані перевіряють по ГОСТ9061

Затискна сила, що розвивається ексцентриком

;

де φ1 – кут тертя на осі ексцентрика

При довжині рукоятки (l≈2D)  розрахунок можливо проводити по формулі:

W=12Q

Для визначення залежності між силою затиску Qі моментом на рукоятці ексцентрика розглянемо, які сили діють на закріпленні деталі (рисунок 5б).

Діють три сили – сила на рукоятці N, реакція заготовки T і реакція заготовки S. Під дією цих сил система знаходиться в рівновазі.

Сума моментів усіх сил, які діють відносно повороту ексцентрика

Nl – Q e sin á – fQ (R +e  cos á) – Sρ = 0;

де  f –коефіцієнт тертя ковзання між ексцентриком і заготовкою

Так як сила S мало відрізняється від нормальної сили Q, приймаємоS≈Q, тоді

Nl = Q [ f R + ρ+e (sin á + f cos á)];

спрощуємо і получаємо

Nl = Q [R sin φ + ρ + e sin (á+φ)];

підставляємо замість R  його значення получимо

;

звідки            Nl=M;

За допомогою полученної приблизної формули можливо визначати момент з точністю до 10%.      

       Конструкції ексцентриків                    

                       а)                                                                             б)

в)                                                                          г)

а – круглий;  б – вильчатий; в –кулачковий одинарний; г - здвоєний

Комбіновані затискачі

1 – гайка

2 – опорний палець

3 – заготовка

4 – пружинний прихват

5 – гвинт

6 – ексцентрик

7 – опора ексцентрика

Рисунок 6 – Нормалізований комбінований прихват

На рисунку 6 показаний комбінований пристрій, який складається з гвинтового і ексцентрикового затискача.

          Важільні – так як і клинові, застосовуються в сполучені з другими елементарними затискачами. За допомогою важелю можливо міняти величину і напрямок передаваємої сили, а також здійснювати одночасно і рівномірно закріплення заготовки в двох місцях.

                   

Рисунок 7 – Схема дії сил у важільних пристосуваннях

Сили Q - початкова і W - затиску будуть різні

Реакція N на вісі важеля, від неї виникає сила тертя Nf, яка діє на зустріч обертанню.

Рівняння рівноваги важеля відносно точки О1без сил тертя :

 

Звідси            ;

або                             N=Q+W   - без сили тертя

З силою тертя рівняння  і відношенням сил : початкової від механізованого привода і затиску деталі

;

звідки

;

Сила затиску -  

Введемо в формулу замість N  його значення, тоді після перетворення сила затиску

або

                                       

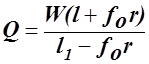
Важільні механізми застосовуються у вигляді притискних планок у гвинтових та ексцентрикових затискуючих устроїв.

Три схеми розрахунку діючих сил затиску:

1)

1 –  деталь, що затискують

2 – точка опори важеля

Q – початкова сила, яку розвиває гвинт або ексцентрик, або шток привода.

η - ккд, що враховує затрати на тертя в опорі важеля (η =0,95)

З рівності моментів сил відносно опор знаходимо

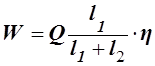
Якщо                       ,      то

2)

;

при        W=2Qη

3)           

                                                                    

при       W=Qη

 3 Силу затиску конструктор розраховує з врахуванням того, що при обробці на заготовку діють наступні сили:

1 – сили обробки – вони носять непостійний ударний характер;

2 – об’ємні сили – вага заготовки, відцентрові сили і інерційні;

3 – сили другорядного і випадкового характеру, які виникають при відведенні робочого інструменту, сили опору тощо.