Решение дифференциального уравнения посредством функций odesolve(t,tК,m) и rkfixed(Z0, t0, t1, m, D). Преобразование нулевых начальных условий при построении переходного процесса в САУ на скачок задающего воздействия. Исследование устойчивости САУ 2–го порядка с периодической нелинейностью на основе построения динамических процессов вблизи границы устойчивости.
Ключевые термины раздела 7.
автоколебания 2-го рода – автоколебания САУ с периодической нелинейностью, когда ее выходная величина непрерывно увеличивается, получая за каждый период автоколебаний приращение 2p (см. разд. 7.2.3).
ДИНАМИЧЕСКИЕ ПОКАЗАТЕЛИ КАЧЕСТВА САУ – параметры переходного процесса при единичном скачке задающего воздействия в начальный момент: время подъема tп выходной величины х(t) САУ до заданного уровня УП с дальнейшим пребыванием процесса выше этого уровня, максимальное перерегулирование sм в процентах от установившегося значения выходной величины, время регулирования tp – время входа процесса х(t) в полосу статической ошибки D САУ, количество колебаний Nк в промежутке 0 – tp, частота колебаний Wк.
начальные условия единичного скачка – начальные условия, возникающие в САУ при t = +0 при скачкообразном единичном задающем воздействии при t = 0 и нулевых начальных условиях (см. разд. 7.1.1).
решатель дифуравнения – совокупность объектов Mathcad, обеспечивающих решение дифуравнения..
устойчивость сау с периодической нелинейностью «в большом» – устойчивость при любых, сколь угодно больших начальных отклонениях фазовых координат САУ от стационарного состояния (см. разд. 7.2.3).
Описание функции – поз.1 табл. 7.1. Пример применения показан на рис. 7.1.
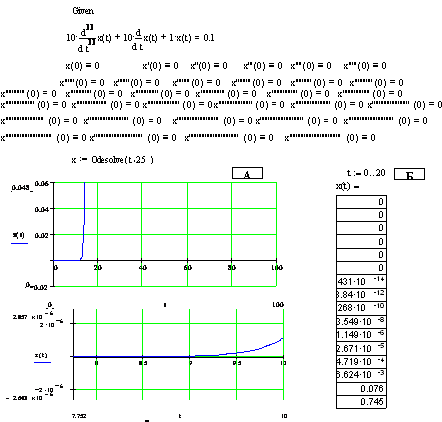
(7.1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.