Данная функция применяется для решения системы обыкновенных дифференциальных уравнений первого порядка. При использовании этой функции для решения одного дифуравнения n-го порядка или системы дифуравнений не первого порядка их нужно привести к системе дифуравнений первого порядка введением в структуру системы выражений присвоения дополнительных переменных для младших производных.
Описание функции – поз. 2 табл. 7.1. Решаемое уравнение (7.14) с нулевыми начальными условиями. Фактически вместо (7.14) используется усеченное уравнение – (7.15) с пересчитанными начальными условиями по формулам (7.12).
Порядок решения
Дифуравнение n-го порядка (7.15) заменяется расчетной системой n дифуравнений 1-го порядка (7.17), решением которой является вектор у с числом компонентов, равным порядку n решаемого уравнения.. Расчетная система
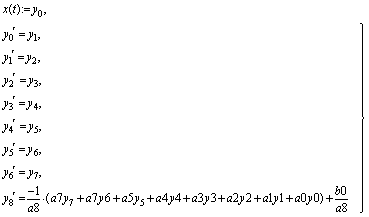
(7.17)
носит поясняющий характер, и может не вводиться в рабочий документ Mathcad.
Следующие этапы показаны на рис. 7.4.
1. В РДМ вводится усеченное дифуравнение, соответствующее уравнению (7.14): усеченные элементы видны из сравнения двух уравнений – (7.14) и уравнения из этапа 1. Уравнение используется как справочное для вычисления части начальных условий, ставших ненулевыми, и для формирования системного вектора D(t,y).
2. Ввод коэффициентов дифуравнения (7.14), включая и коэффициенты усеченных членов.
3. Расчет по
формулам (7.12) значений ненулевых производных – 5-й, 6-й и 7-й. Слева и ниже
от выражений производных – их численные значения. В выражениях производных: ![]() .
.
4. Ввод вектора начальных условий для у: его длина равна порядку уравнения, т.е. 8.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.