Решение обыкновенных дифференциальных уравнений (задача Коши), страница 16

n^нус_гр = 0, 3224 и измерение их параметров Т_пер, x¢_max , x¢_min посредством панельки Trace

стрелками по точкам графика впадины для выявления минимального значения, которое записывается через буфер в матрицу W1.

6.  Повторите п. 4 и 5 для всех заданных значений q.

7.  Уничтожьте столбец q в матрице W1 и объедините матрицы W1 и W2 командой «augment(W2,W1)», вставив ее в присвоение для имени ИТИ (Итоговая Таблица Исследования). Введите новое присвоение для име­ни ИТИ1 и вставьте в него содержание таблицы ИТИ через команду«Copy Selection». Уничтожьте в таб­лице ИТИ1 строку заголовка через панельку Insert Matrix.

8.  Постройте график найденной границы с разметкой осей по таблице ИТИ1, согласно рис. 7.8. Вызовите панельку Форматирование выделенного Графика  и через оконца вкладки labels введите текстовые подписи для осей и название графика.

                                                                                                       

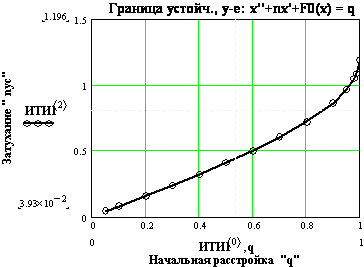
Рис. 7.8. Оформление графика грани­цы устойчивости в «в большом» для САУ с уравнением (7.19) в РДМ

7.3. Упражнения

Выборочные упражнения

№ п/п	Задание	Методика, номер раздела	Источник данных
1	Вычисление переходного процесса в САУ решателем given …odesolve при единичном скачке задающего воздействия с преобразованием нулевых нач­условий к ненулевым, построение графика.и вычисление показателей качества переходного процесса по графику.	7.1.1, рис. 7.3	Разд. 15.8.1, табл.15.8.1
2	Вычисление переходного процесса в САУ решателем rkfixed и построение графика.	7.2.1, рис. 7.4	Разд. 15.8.1, табл.15.8.1
3	Решение дифуравнения «замечательной» кривой и построение графика решения в полярных координатах со вставкой подписи и обозначений	7.2.2, рис. 7.5	Разд. 15.8.2, табл.15.8.2, любой вариант из раздела «Дифуравнение розы»
4	Построение границы области устойчивости «в большом» САУ с периодической нелинейностью, вставка подписи к рисунку области и обозначений.	7.2.3, рис.  7.6…7.8	Разд. 15.8.4, табл.15.8.4, Приложение 3 «Периодические Функции …»