Решение обыкновенных дифференциальных уравнений (задача Коши), страница 14

·  n^ус_гр –  значение n с устойчивым процессом;

·  n^нус_гр – значение n с автоколебаниями 2-го рода,  n^нус_гр =  n^ус_гр –0,0001;

·  Т_пер – период автоколебаний 2-го рода;

·  x¢_max – значение x’ в точке максимума волны автоколебаний 2-го рода (измеряется инструментом Trace Mathcad );

·  x¢_min  - значение x’ в точке минимума волны автоколебаний 2-го рода;

·  _Lскач  - количество 2p - скачков разности фаз при переходе из начального положения в конечное при n^ус_гр .

Этапы проведения исследования

1.  Составляется решатель Mathcad для уравнения (7.19), который обеспечивает решение дифуравнения для вручную изменяемых параметров n и q (в (7.18) указаны конкретные значения для одной из точек границы).

Внимание! Первая строка Решателя и вектор D(t,y) должны быть модифицированы в соответствии с функцией F0(x) Задания.

 

                                                                                                                                                                          (7.21)

2.  Создайте матрицы – заготовки W1 и W2 для данных исследования, аналогичные матрицам (7.22), и расположите их выше Решателя для удобства манипуляциями настройками при исследовании (разбиение на две матрицы связано с тем, что Mathcad 13 не может создать в ручном режиме матрицу большего размера, чем W1, – зато объединить заполненные обе матрицы в единую расчетную таблицу он может – см. п. 7).

Матрицы имеют вид

 

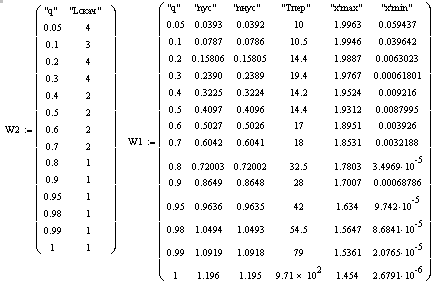
                                                                                                                                                                           (7.22)