Решение обыкновенных дифференциальных уравнений (задача Коши), страница 4

7.1.1. Построение переходного процесса в системе автоматического управления при единичном скачке задающего воздействия

Такой процесс строят для определения динамических показателей качества САУ (см. термины в начале разд. 7). Начальные условия у процесса нулевые. В общем случае скачок задающего воздействия на пути от входа к выходу САУ подвергается дифференцированию разного порядка, в результате которого возникают дельта-функции, длительность которых равна нулю, а амплитуда – ± ¥ (см. выражение (7.5)). Реализовать такие функции на компьютере невозможно. Поэтому, вместо единичного скачка в расчете используют постоянное еди­ничное задающее воздействие, в результате чего устраняется влияние дифференцирования задающего воздействия. Чтобы переходные процессы обоих воздействий совпадали, начальные условия переходного процесса при постоянном единичном воздействии делают ненулевыми.

7.1.1.1. Преобразование нулевых начальных условий единичного скачка к                                                                                       начальным условиям постоянного единичного воздействия

Пусть передаточная функция замкнутой системы при нулевых начальных условиях имеет вид (s – параметр преобразования Лапласа переходных процессов в САУ):

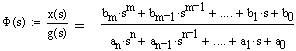
                                                             .                                                                                        (7.2)

Тогда дифуравнение переходного процесса в САУ при любом входном воздействии g(t) имеет вид:

                                                                                                                                        ,  m £ n  ,              (7.3)

где р =        – оператор дифференцирования, рⁿ =        .

Пусть g(t) является единичным скачком, т.е. g(t) = 1(t) = 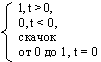                                                                    (7.4)