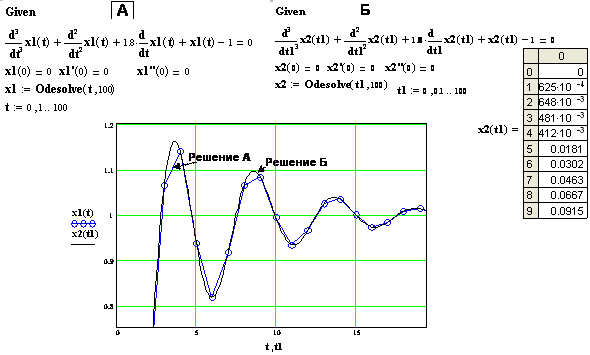
11. Решение х(t) не выводится в виде таблицы, но его можно визуализировать, применяя графический блок Mathcadа – см. рис. 7.1А. Для вывода решения в виде таблицы необходимо ниже функции odesolve ввести диапазон аргумента t, для которого выводится решение (этот диапазон не должен превосходить диапазон в самой функции odesolve), и конструкцию вывода (расчета): х(t) = (см. рис. 7.1,Б).
12. Для того, чтобы при заданном tK увеличить точность воспроизведения х(t) посредством увеличения количества шагов m необходимо произвести вывод таблицы решения из п. 11, предусмотрев в диапазоне t аргумента таблицы нужное количество шагов (см. рис. 7.2: количество шагов для кривой х2 (решение Б ) увеличено в 10 раз по сравнению с х1(решение А )).
 |
(7.1Б)
Рис. 7.2. Увеличение точности решения дроблением шага (для t1), вводимом ниже решающего блока Given – odesolve. Шаг х2 (решение Б) в 10 раз меньше, чем у х1 (кривой с кружками - решение А)
Таблица 7.1
Ряд функции Mathcad 13 для решения обыкновенных дифференциальных уравнений (задачи с начальными условиями – задачи Коши)
|
Вид функции, назначение |
Условия применения |
Аргументы |
|
1. odesolve(t, tk, число шагов m). Интегрирование одного обыкновенного дифуравнения n-го порядка с начальными условиями методом Рунге - Кутта 4-го порядка с фиксированным шагом (по умолчанию) или с переменным шагом (команда adaptive в меню от правой кнопки мышки на имени odesolve). Выдает функцию у(t) – решение уравнения: увидеть эту функцию можно только в графическом блоке; значение функции при выбранном аргументе определяется посредством измерительной панельки X-Y Trace, вызываемой при выделенном блоке через меню Формат-Граф-Трасса. |
В решающем блоке, открываемом оператором Given, ниже которого записывается дифуравнение, граничные условия и ограничения – равенства, и закрываемом функцией odesolve (см. рис. 7.1). Наивысшая производная должна быть линейной функцией. |
t – действительная переменная. b – действительное число. Z0 – вектор начальных значений функции у(0) и ее производных вплоть до у ( n -1)(0) при решении одного дифуравнения или вектор начальных значений уi (0) (i = 1…n) при решении системы n дифуравнений. t0, t1 –начальная и конечная точки интегрирования. m – число точек на интервале t0 – t1 (не считая начальной), в которых выдается решение дифуравнения. D – системный n-элементный вектор решаемого уравнения или системы уравнений, элементы которого равны правым частям системы n дифуравнений 1-го порядка решаемой системы или созданной из дифуравнения n-го порядка приведенной системы (см. 0рис. 7.2). J – функция, выдающая n×(n+1) – матрицу, первый столбец которой содержит производные, а в остальных строках и столбцах записан Якобиан приведенной системы решаемого дифуравнения. acc – управляет точностью решения; значение acc = 0, 001 достаточно для обеспечения высокой точности результата. kmax – максимально допустимое число точек, в которых производиться аппроксимация решения, одновременно это и число строк матрицы, выдаваемой выбранной решающей функцией п. 7. s – нижнее значение различия двух соседних чисел в первом столбце матрицы, выдаваемой решающей функцией п.7. |
|
2. rkfixed(Z0, t0, t1, число точек m, D).Альтернативный п.1 метод интегрирования одного обыкновенного дифуравнения n-го порядка с начальными условиями методом Рунге – Кутта 4-го порядка. Выдает матрицу с числом строк m+1, первый столбец которой – значения t, второй – у(t), третий – у¢(t), последующие - значения остальных производных вплоть до (n – 1)-го порядка. |
Вектор Z0 начальных значений функции у(0) и ее производных вплоть до у ( n -1)(0) и системный n-элементный вектор D решаемого уравнения должны быть введены раньше функции rkfixed. Наивысшая производная может быть нелинейной функцией. |
|
|
3. rkfixed(Z0, t0, t1, число точек m, D). Метод интегрирования системы n обыкновенных дифуравнений 1-го порядка с начальными условиями методом Рунге – Кутта 4-го порядка с фиксированным шагом. Выдает матрицу с числом строк m+1, первый столбец которой - значения t, второй – у1(t) , третий – у2(t) , последующие – значения остальных функций уi(t) вплоть до n-й. |
Вектор Z0 начальных значений уi (0) (i = 1…n) и системный n-элементный вектор D, состоящий из правых частей решаемой системы, должны быть введены раньше функции rkfixed. |
|
|
4. Bulstoer(Z0, t0, t1, число точек m, D). Интегрирование одного обыкновенного дифуравнения n-го порядка с начальными условиями методом Булирш – Стоера, который немного точнее метода Рунге - Кутта для гладких решений. Выдает матрицу с числом строк m+1, первый столбец которой – значения t, второй – у(t), третий – у¢(t), последующие значения остальных производных вплоть до (n – 1)-го порядка. |
Вектор Z0 начальных значений уi (0) (i = 1…n) и системный n-элементный вектор D, состоящий из правых частей решаемой системы, должны быть введены раньше функции bulstoer |
|
|
5. Stiffb(y, t0, t1,число точек m, D, J), Stiffr(Y, t0, t1,число точек m, D, J). Для жесткой системы. Интегрирование одного обыкновенного дифуравнения n -ого порядка с начальными условиями методом Булирш – Стоера (для первой функции) и методом Розенброка (для второй). Выдает матрицу с числом строк m+1, первый столбец которой – значения t, второй – у(t), третий – у’(t), последующие - значения остальных производных вплоть до (n – 1) -го порядка. |
Вектор Z0 начальных значений уi (0) (i = 1…n) и системный n-элементный вектор D, состоящий из правых частей решаемой системы, должны быть введены раньше функции Stiffb или Stiffr. |
|
|
6. Rkadapt(y,t0, t1,число точек m , D). Для медленно меняющейся системы. Метод интегрирования одного обыкновенного дифуравнения n-го порядка с начальными условиями методом Рунге – Кутта 4-го порядка с переменным шагом, адаптируемым к скорости изменения решения. Выдает матрицу с числом строк m+1, первый столбец которой – значения t, второй – у(t), третий – у¢(t), последующие - значения остальных производных вплоть до (n – 1)-го порядка. |
Вектор Z0 начальных значений уi (0) (i = 1…n) и системный n-элементный вектор D, состоящий из правых частей решаемой системы, должны быть введены раньше функции Rkadapt |
|
|
7. bulstoer(y, t0, t1, acc, D, kmax, s), rkadapt(y, t0, t1, acc, D, kmax, s), stiffb(y, t0, t1, acc, D, J, kmax, s), stiffr(y, t0, t1, acc, D, J, kmax, s). Все функции выдают решение в конечной точке t1 заданного интервала согласно свойствам, указанным выше для каждой одноименной решающей функции. |
Согласно условиям применения соответствующей решающей функции. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.