Решение обыкновенных дифференциальных уравнений (задача Коши), страница 12

5.  Ввод системного вектора D(t,y). Его компоненты являются правыми частями системы (7.17). Знакоместо для индексов у компонент вектора у вводится кнопкой  х_n  c панельки Matrixили клавишей <{ [>. 

6.  Ввод решающей функция rkfixed через присваивание (например, имени « z») с аргументами: вектор у, начальное и конечное значения переменной интегрирования t (0 и 60 c – для решаемого примера), число шагов (1000) и имя вектора D (без аргументов).

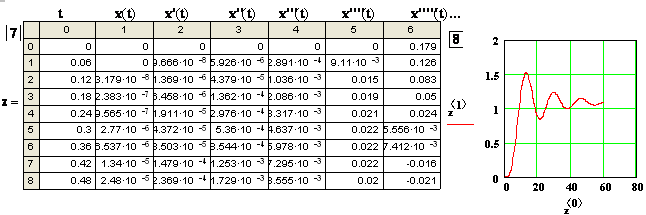
7.  Командой «z =» выводится выходная таблица решения системы уравнений (7.17), столбцы которой (с нулевого по восьмой): переменная t, решение у₀(t) (x(t)) , первая,  вторая  и т.д. производные решения (вплоть до 7-й)..

8.  Вывод решения у₀(t) (x(t)) на график следует производить с учетом значений столбцов таблицы решения: на оси абсцисс – нулевой столбец, на оси ординат – 1-й.

 

Рис. 7.4. Решение дифуравнения (7.14) при единичном скачке задающего воздействия g(t) с преобразованием уравнения в систему (7.17) и использованием решающей функции rkfixed(…). Апострофы в производных вводятся сочетанием клавиш <Ctrl>+<F7>

 

Продолжение рис. 7.4

7.2.2. Решение  дифференциального уравнения «розы»                                          с применением функции rkfixed

Дифуравнение розы имеет вид

у¢¢¢(v) = –ak³ cos(kv),                                                                                                   (7.18)

где а – радиус, описанной вокругрозы окружности; k – количество лепестков.