Решение обыкновенных дифференциальных уравнений (задача Коши), страница 15

3.  Вставьте два графических блока с разметкой, аналогичной рис. 7.6. Над  графическими блоками вставьте два вычислительных блока «Т : = а – b»  и «Т : = » для вычисления периода автоколебаний 2-го рода.

4.  Заполните  столбцы q заданными значениями q в матрицах W1 и W2. Вставьте одно выбранное значение q в Решатель. Меняя значения «n» в Решателе,  найдите  значения nус и nнус (ориентируясь по данным матрицы W1 в (7.20)); при этом, картина процессов для n = nус должна быть похожей на рис. 7.6, а для nнус = nус + D (D - заданная вам точность, например 0,0001) должна походить (после применения средства « Zoom» к правому графическому блоку) на рис. 7.7. Запишите найденные значения в матрицу W1.  

 

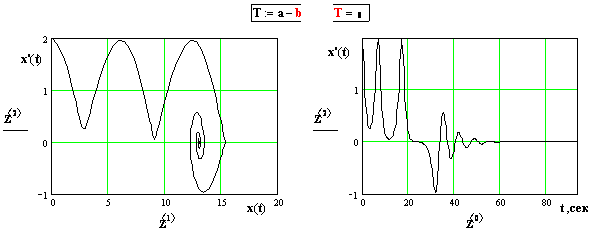Рис. 7.6.  Графические блоки для исследования уравнения  (7.20). Процессы в точке q = 0. 4,   

n^ус_гр = 0,3225; Lскач = 2 (для этой точки  n^нус_гр = 0, 3224).

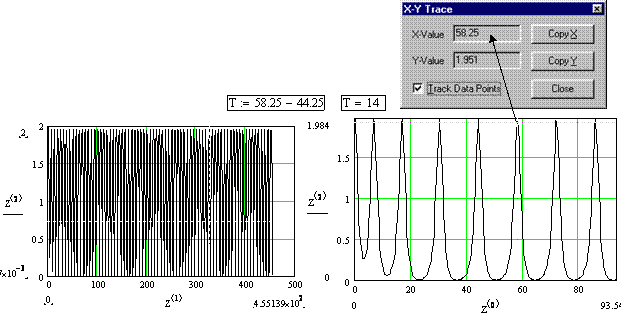
5.  Вставьте найденное значение n = nус в Решатель и определите на левом графике количество 2p-скачков Lскач, записав это значение в матрицу W2. Замените в Решателе nус на nнус и измерьте параметры автоколебаний с помощью панельки Trace и операций буферного копирования и вставки (см. рис. 7.7):

·  Т – определяется по двум соседним вершинам волн путем копирования в буфер значений х и вставки их в соответствующие места вычислительного блока  Т : = а – b;

·  x¢_max – определяется по вершине волны, копируется в буфер и вставляется в матрицу W1;

·  x¢_min – определяется посредством помещения курсора во впадину между вершинами с последующим сканированием клавишами со

Рис. 7.7.  Автоколебания 2-го рода в точке границы устойчивости «в большом» для q = 0. 4 и