Решение обыкновенных дифференциальных уравнений (задача Коши), страница 5

При подстановке 1(t) в правую часть (7.3) и дифференцировании получим:

р1(t) = d(t) = 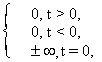                                   р^m1(t) = d^{(m -1)}(t) =  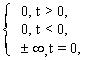                                                                        (7.5)

d(t), d^{(m -1)}(t) – дельта - функция и ее (m –1)-я производная.

Выходную переменную х(t) представим в виде

х(t) = х1(t)×1(t) = х(t)×1(t) (для упрощения записи х1 вновь заменяем на х) .                                               (7.6)

Подставляя х(t) из (7.6) и g(t) из (7.4) в (7.3),  получим для t > 0  усеченное дифференциальное уравнение переходного процесса в САУ при единичном постоянном воздействии на входе, соответствующее дифуравнению САУ (7.3) при единичном скачке на входе, которое с учетом (7.4), (7.5) имеет вид:

                                                                  = b₀ , t > 0.                                                                                         (7.7)

При t = 0 происходит скачкообразное изменение нулевых начальных условий в САУ из-за дельта-функции и ее производных от входного воздействия (назовем их  измененными начальными условиями единичного скачка), и получим следующее уравнение для определения измененных начальных условий с учетом (7.5):

                                                         ×1(t) = b_m×d^{(m -1)}(t) + b_m-1×d^{(m -2)}(t) + ××× + b₁×d(t) + b₀, t = 0,                (7.8)

причем,

р[x(t) × 1(t)] = х ⁽¹⁾(t)1(t) + х(t) ×d(t) = х ⁽¹⁾(0) + х(0) ×d(0),                                                                                (7.9)     

рn[x(t) × 1(t)] =            ×d^{(n -m - 1)}(t) х^(m)(t) + 1(t) х⁽ⁿ⁾(t) =            ×d^{(n -m - 1)}(0) х^(m)(0) + х(n)(0),