Построение и преобразование структурных схем, описывающих систему управления. Дифференциальные и алгебраические уравнения, страница 17

Алгебра Кронекера призвана перевести в линейную область операции выше первой степени.

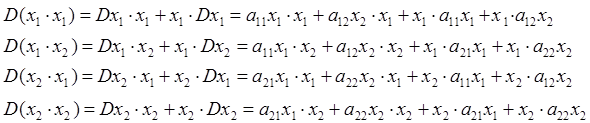
Пусть  - умножение по Кронекеру:

 

Мы должны получить следующий результат:

, где

,

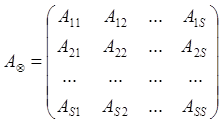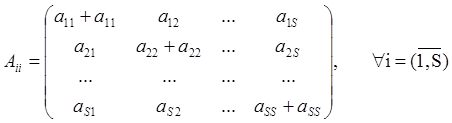
Все матрицы А_ii одинаковые.

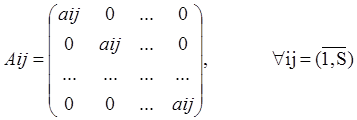
Все матрицы А_ij разные.

Введем обозначение:

,     

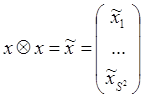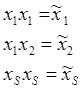
Число переменных было S, стало S².

Обозначим , тогда получим ДУ первого порядка, которое мы можем дифференцировать:

.

К этому уравнению можно добавить уравнение выхода:

, где

- матрица, которую составим таким образом, чтобы на выходе получить произведение с одинаковыми индексами. Такой матрицей является прямоугольная диагональная матрица С, где на первом месте стоит единица. В нашем уравнении матрица С второго порядка:

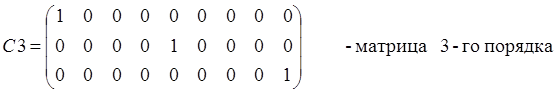
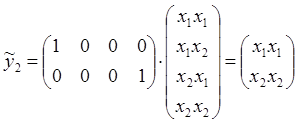
13.05.99

Dx1=a11x1+a21x1

Dx2=a21x2+a22x2          x(t₀)=x0

Произведение Кронекера получается умножением матрицы слева на матрицу справа поэлементно с записью результата на место каждого элемента правой матрицы.

       

           

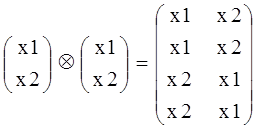
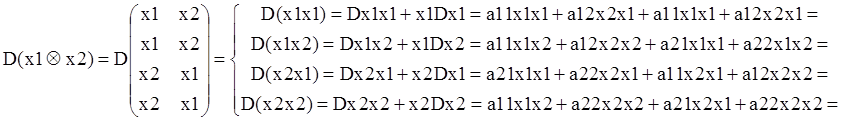
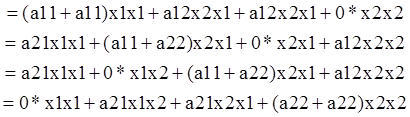
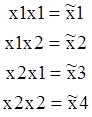
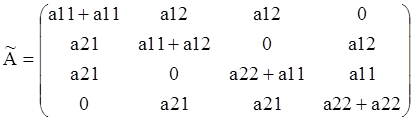
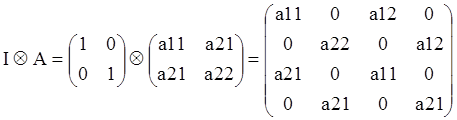
     ,где -сложение по Кронекеру (внашем случае оно совпадает с обычным сложением)

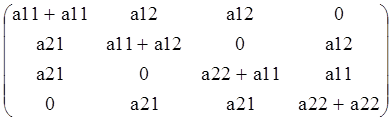
Если удасться проинтегрировать это уравнение, мы получим решение ДУ относительно каждой переменной состояния .

Всё это делали для того, чтобы определить         

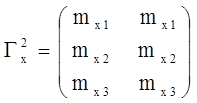
Произведение двух переменных состояний Г_х² должны быть больше 0, так как это второй момент. А это может быть только тогда, когда индексы у переменных одинаковы. Все остальные переменные состояния могут заходить в отрицательную полуплоскость.

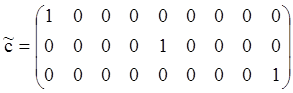
после чего определяется задача: 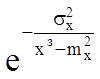 , где х^з – «х» заданное.

Для оценки качества определим следующие понятия:

1.  Функциональный запас по показателю функционирования J_m для

 , где вектор J – это вектор показателей функционирования

J=(J₁,…J_m,…J_M)^T

J³ – заданное значение. Бывает двух видов:

J^гр – граничные значения, которые опреедляют область эффективной эксплуатации любой ДСУ(динамической системы управления)

J^пр – предельные значения, которые определяют область безаварийной эксплуатации и явяляются её границей/

2.  Вероятность безотказного функционирования (ВБФ) или функциональная безотказность.

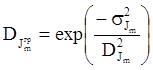
Для этой функции выражение функционального запаса выглядит след. образом:

3.  Вероятность безопасного функционирования или функциональная безопасность.

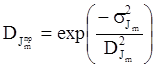, а функциональный запас

4.  Каждой ДСУ свойственна оценка надёжности, самой существенной оценкой, которая обеспечивает эффективность достижения этой системой предписанной ей целевой функции является вероятность безотказной работы (ВБР)

          

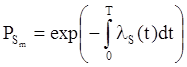
m определяет тот канал, который обеспечивает реализацию показателя J_m

5.  Если из ВБР взять значения интеграла и обозначить его ,

То -вероятный отказ схемно-конструктивной реализации.

6.  Если взять производную справа и слева по времени (это возможно, т. к. является интегралом по времени), то получим интенсивность схемно-конструктивных отказов.

Понятия № 4, 5 и 6 определяют показатели надёжности функционирования ДСУ.

Если вернуться к определениям № 2 и 3, то мы обнаруживаем, что форма записи вероятности полностью совпадает с вероятностью безотказной (безопасной работы) схемно-конструктивонй вероятности. Отсюда вытекает ещё одно определение.

7.  Вероятностный отказ безотказного и безопасного функционирования  в зависимости от значения J³ (J^гр и J^пр) в выражении функционального запаса.

 Это возможно, т. к. J_Jm²  является функцией времени.

8.  Интенсивность функциональных отказов эффенктивной и безопасной эксплуатации в зависимости от заданных значений функциональных запасов J³

            x(t0)=x0

-внешнее воздействие (бывают управляющие и возмущающие). Управляющие воздействия надо регулировать с максимальной точностью.

-это уравнение второго закона Ньютона, которое описывает абсолютное движение (всего три вида движений: абсолютное, переносное и относительное)….

Проверкой того, что задача решена правильно, является то, что  не может заходит в отрицательную плоскость.

Мы рассматривали матрицу А, не зависящую от μ.

.