· заданных значений
Jз, которые могут состоять из:
Jгр – область, где эффективно работает наша система,
Jпр – определяет безаварийную ситуацию.
Введем заданное значение в виде:
![]()
определяет разницу между заданным математическим ожиданием и математическим ожиданием для всей гаммы таких ФЗ для каждой системы М-штук.
Для исполнения (*) для оценки качества
1.
2. n —> ∞ => вместо скобки получим е.
PFJm – вероятность безопасного (или безотказного?) функционирования по показателю Jm.
- безопасность (безотказность) функционирования.
когда в DJm J3m = Jпр или J3m = Jгр
J п/р:
надо решить уравнение относительно σх2, для этого можно решить:
![]()
![]()
Проблема: σ2 : при х=0, σх02=0, следовательно мы не можем получить стахо.
! Решать надо другое уравнение:
2. DГх2 = Гх2; Гх2(t0) = Гх02
Г2 – второй начальный момент из 1. Dmx получим mx установившееся
из 2. Гх2 получим Гх уст.2.
![]()
Осреднение простого уравнения:
![]()
![]() х,
х, 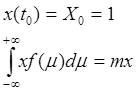 Т.
к. решением этого дифференциального равнения:
Т.
к. решением этого дифференциального равнения:![]()
![]()
![]()
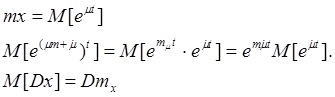
т.к. операция осреднения - линейная операция, следовательно, порядок их может быть изменен:
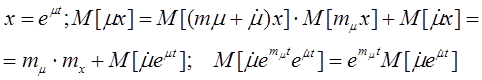
![]() вынесем
mx за скобку.
вынесем
mx за скобку.
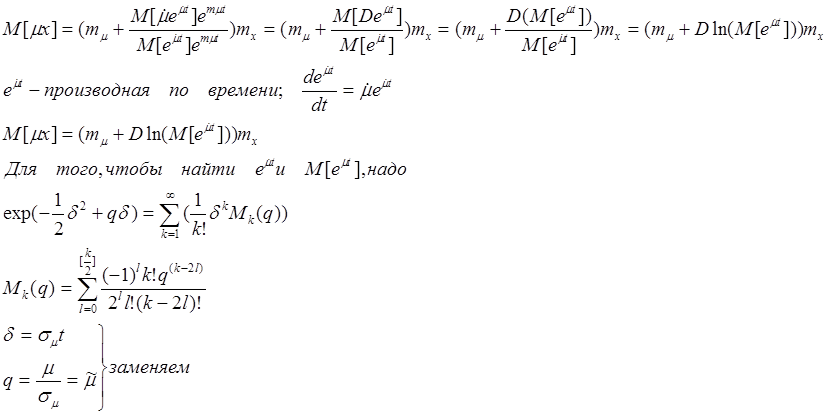
Контрольный вопрос: Чему равняется ![]() ?
?
29.04.99
Если в первом уравнении ![]() задать
некоторой неизвестной функцией времени, например 1(t),
то из решения системы 15-ти уравнений можно определить функции времени для всех
переменных.
задать
некоторой неизвестной функцией времени, например 1(t),
то из решения системы 15-ти уравнений можно определить функции времени для всех
переменных.
![]() (*)
(*)
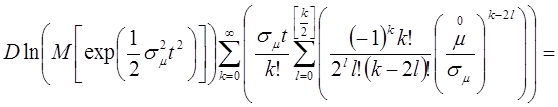
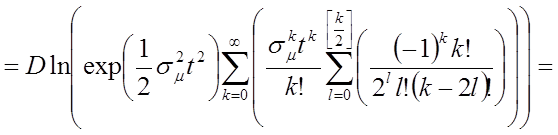
Зная, что 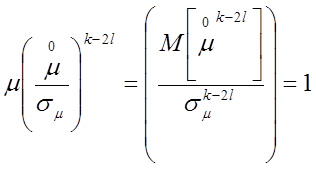 ,
получаем:
,
получаем:
![]()
![]()
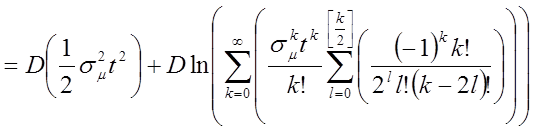
![]()
![]()
![]()
![]()
Это коэффициент при переменной для ур-я (*)
![]() -
это функция от времени, следовательно это уравнение потеряло стационарность.
-
это функция от времени, следовательно это уравнение потеряло стационарность.
Исходное уравнение, которое мы осредняли имело вид: ![]() -
это дифф-е уравнение 1-го порядка стационарно-стахостическое (
-
это дифф-е уравнение 1-го порядка стационарно-стахостическое (![]() не
зависит от времени, след-но стационарние. И оно носит случайный характер, т.к.
характеризуется
не
зависит от времени, след-но стационарние. И оно носит случайный характер, т.к.
характеризуется ![]() и
и
![]() ,
а след-но оно стахостическое)
,
а след-но оно стахостическое)
На рисунке ![]() имеет
равномерный закон распределения
имеет
равномерный закон распределения
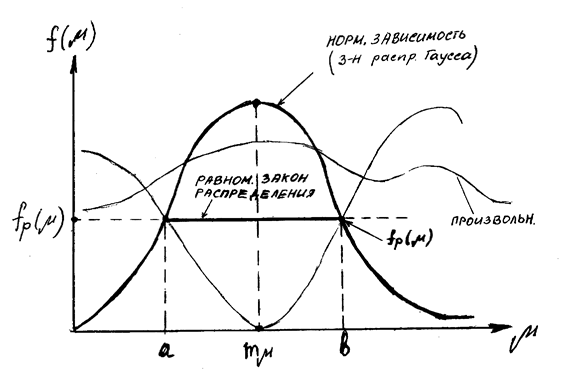
РИС. “РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ”
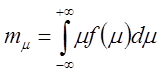
![]() , т.к.
, т.к. 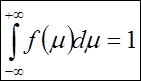 -
основной закон теории вероятностей.
-
основной закон теории вероятностей.
Из этого закона следует, что мат. ожидание и дисперсия для равномерного закона имеют вид:
![]() ;
; 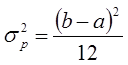
Коэффициент передачи ![]() является
функцией времени, следовательно в результате осреднения исходного стационарного
уравнения относительно мат. ожидания исходное уравнение потеряло свойство
стационарности, т.к. его коэффициент передачи стал зависеть от времени. Чтоб
это уравнение было устойчивым необходимо и достаточно чтоб форма его решения была:
является
функцией времени, следовательно в результате осреднения исходного стационарного
уравнения относительно мат. ожидания исходное уравнение потеряло свойство
стационарности, т.к. его коэффициент передачи стал зависеть от времени. Чтоб
это уравнение было устойчивым необходимо и достаточно чтоб форма его решения была:
![]() , при
, при ![]()
![]() -
случайный параметр (должно выполняться условие
-
случайный параметр (должно выполняться условие ![]() ,
тогда
,
тогда ![]() уравнение
станет устойчивым.
уравнение
станет устойчивым.
Если закон распределения нормальный
(величина ![]() отвечает
нормальному закону распределения), то для всех значений
отвечает
нормальному закону распределения), то для всех значений ![]() от
0 до
от
0 до ![]() мат.
ожидание
мат.
ожидание 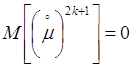 (
нечетные значения) и
(
нечетные значения) и
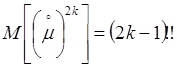 (
четные значения)
(
четные значения)
При этом ![]() ,
а для всех
,
а для всех ![]() =1,2…
=1,2…![]() ,
,
![]()
При нормальном законе распределения ![]() .
Следовательно,
.
Следовательно, ![]() ,
,
при ![]() .
.
Если исходное уравнение устойчиво, то для того чтобы
осредненное уравнение тоже было устойчиво в момент времени t
= 0 необходимо и достаточно, чтобы выполнялось условие ![]() при
t = 0
при
t = 0
Если t = T , и след-но ![]() ,
то
,
то 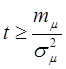 .
(при этом осредненное уравнение теряет свою устойчивость)
.
(при этом осредненное уравнение теряет свою устойчивость)
Реальные, правильно спроектированные,
системы малочувствительны к изменению случайных параметров, т.е. ![]()
Время переходного процесса при
некоторых воздействиях всегда много меньше времени старения (или срока службы)
системы : ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.