Построение и преобразование структурных схем, описывающих систему управления. Дифференциальные и алгебраические уравнения, страница 16

Осредненное уравнение относительно дисперсии:

  - продифф-ть  это уравнение относительно….  (по дисперсии невозможно0

Для получения осредненного уравнения для второго начального момента: , Проведем операцию осреднения:

Применим операцию мат. ожилания:

 и т.д.

  ,    

Самостоятельно провести этот вывод и получить уравнение:

    (по основной теореме теории вероятности)

 - это решение исходного дифф-го уравнения 

В нем можно выдеоить случайную составляющую

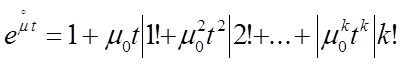   (разложение в ряд Тейлора)

КВ: Какой вид решения  X нужно подставить в исходное уравнение для его осреднения, чтобы реализовать свойство малой чувствительности самого уравнения относительно параметра , если само решение представлено в виде ряда Тейлора?

Ответ:     

30.04.99

07.05.99

Для того, чтобы рассмотреть дифференциальное уравнение (ДУ):

              x(t0)=xo

надо испоьзовать уравнение Сильвестра (умножаем на матрицу из собственных векторов Н):

ΛА – диагональная матрица

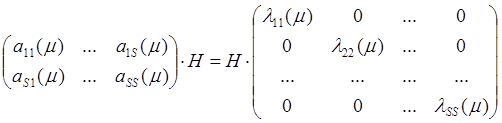, где

λ₁₁, λ_SS – собственные корни характеристического уравнения

Когда появляются комплексные сопряженные корни, появится Джорданова клетка:

Доказательство того, что матрица Н является детерминированной.

Решение ДУ может быть записано:

exp(A(μ)t) – экспоненциал – матрица:

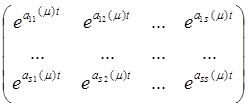          …(1), тогда

x(t)=(1)·xo

Решением ДУ для нашего примера является сумма взвешенных экспонент, при чем их количество S штук, в соответствии с порядком ДУ.

х₀ – начальное условие (их ровно 6 штук, хотя бы одно не должно быть равно нулю).

Так как матрица А, умноженная на Н, превращается в диагональную матрицу, то:

.

Этот экспоненциал имеет достоиноства

–  по диагонали находятся собственные числа

–  для каждой координаты У и соответствующей ей координаты х имеется только одно значение λ_i(μ)t:   

х=Н·У

Y₀ – начальное условие в новой системе координат.

.

Любой из экспоненциалов может быть разложен в ряд из экспоненциалов:

     …(2)

              …(3)

где I – единичная матрица

 .

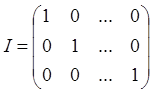Произведем операцию осреднения для уравнений (2) и (3):

 

Раз они детерминированные (т.е. одна получена из другой), для них существует неособенная матрица Е, которая с помощью уравнения Сильвестра переводит матрицу А в диагональную матрицу Λ_А:

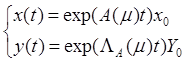
А это возможно только тогда, когда матрица Е тождественна матрице Н:

Е≡Н,

Что и означает, что матрица Н детерминирована. Следовательно, если матрица Н детерминирована, то её можно определить из уравнения математических ожиданий относительно переменных состояний:

Из этого уравнения и получаем детерминированную матрицу Н.

Общие положения:

1.  Для исследования ДСУ определяются общие уравнения состояний свободного движения:

2.  определяются входящие в это уравнение

а) переменные вообще

б) переменные состояний, число которых соответствует порядку математической модели (S) – количество Р в знаменателе передаточной функции разомкнутой системы

в) определяем стохастические параметры μ для всех коэффициентов уравнения

μ – допуска или погрешности, составляющих коэффициент при переменной состояния (разбросы всех постоянных времени и коэффициентов передач); каждая из постоянных времени и коэффициентов передач может быть функцией от μ-случайных параметров.

г) производим операцию осреднения относительно математических ожиданий уравнений состояния свободного движения рассмотренными нами способами. Для определения матрицы Н из этого уравнения рассматриваем начальный момент времени t=0, для которого производится:

Применяем уравнения Сильвестра для матрицы m_А и находим матрицу из собственных векторов Н.

Кроме математического ожидания нас интересует дисперсия . Для её получения необходимо найти уравнения относительно вторых начальных моментов . Вектор может быть записан как:

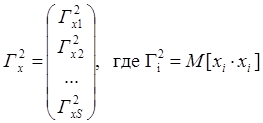
Для того, чтобы найти это выражение, будем использовать алгебру Кронекера.

Рассмотрим пример.