Системы автоматической стабилизации того или иного технологического параметра. Системы автоматического регулирования с запаздыванием, страница 9

Пользуясь этими же ЛЧХ, по номограмме (рис. 9) определяют вещественную частотную характеристику замкнутой системы (рис. 10), которая позволяет оценить качество системы:

,            .

В [5] приводятся рациональные приемы, позволяющие сравнительно просто и с достаточной точностью построить вещественную частотную характеристику (ВЧХ) замкнутой системы.

Если порядок системы равен 3 и передаточная функция не имеет нулей, то в этом случае достаточно эффективным средством оценки устойчивости и качества САР являются диаграммы Вышнеградского [ 2, 5], которые позволяют с наименьшими затратами провести анализ таких систем.

Для астатических систем, наклон логарифмической амплитудно-частотной характеристики (ЛАЧХ) которых является типовым (табл. 1) эффективным окажется применение номограмм качества [5] , которые широко используются в инженерной практике.

Оценка точности САР в установившемся режиме от суммарного действия управляющих и возмущающих воздействий принципиальных трудностей не вызывает и широко освещена в литературу [1 - 5].

При оформлении пояснительной записки по этому этапу курсовой работы необходимо:

дать аргументированное обоснование выбора метода анализа;

привести необходимые выкладки при исследовании устойчивости и запасов устойчивости системы;

привести необходимые выкладки при оценке точности САР в установившемся режиме;

провести сравнительный анализ качества исходной САР с требуемыми показателями качества.

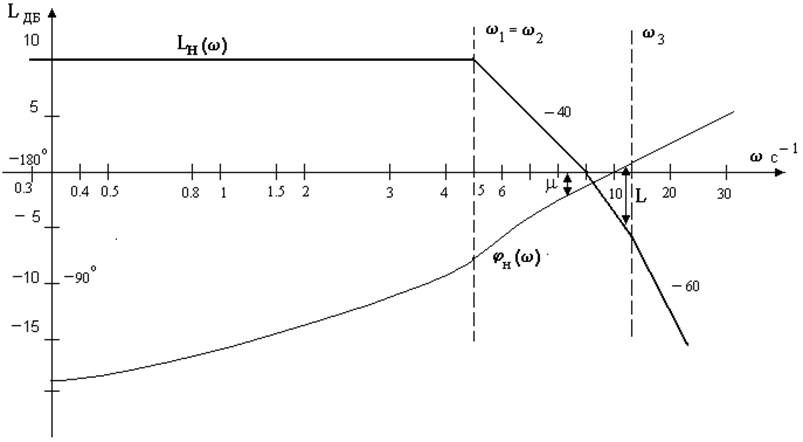Рис. 8. Логарифмические частотные характеристики системы.

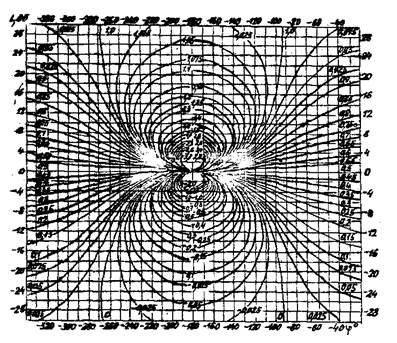
Рис. 9. Номограмма для определения действительной частотной характеристики замкнутой САР по ЛАХ и ЛФХ разомкнутой системы.

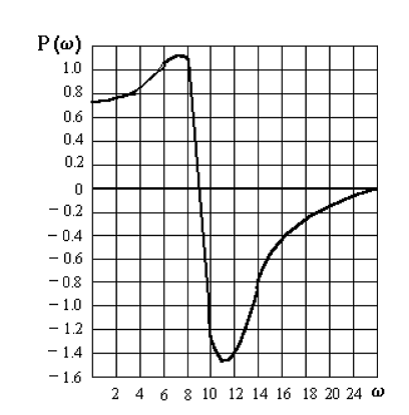
Рис. 10. Вещественная частотная характеристика исходной замкнутой системы.

Таблица 1

Типовые логарифмические амплитудно-частотные характеристики

5.3 Синтез корректирующего устройства

На этом этапе следует выбрать метод синтеза корректирующего устройства, способ его включения, определить его структуру, параметры, а также рассчитать электрический аналог.

Среди возможных методов синтеза можно выделить основные частотные и корневые методы [9], к которым следует добавить еще интегральные методы. Интегральные методы [5], как и корневые, применяются при расчете параметров уже выбранной структуры корректирующего устройства или типового регулятора, в силу этого они менее универсальны и имеют ограниченное применение.

Среди частотных методов различают методы прямых и обратных расширенных частотных характеристик [1-3, 5-8, 12] и методы логарифмических частотных характеристик. Первые два нашли широкое распространение в инженерной практике при синтезе настроек регуляторов заданной структуры [10, 11].

При синтезе по методу ЛЧХ творческим этапом является выбор способа включения корректирующего устройства, структура и параметры которого будут определены в самом процессе синтеза.

При выборе корректирующего устройства прежде всего следует обратить внимание на соотношение между ЛАХ исходной и ЛАХ желаемой систем. Поэтов первым шагом при решении задачи коррекции является построение ЛАХ желаемой системы.

Во всех этих методах используется последовательность расчета в три этапа:

1) формирование низкочастотной части желаемой ЛАХ исходя из требований к точности;

2) построение среднечастотной части желаемой ЛАХ по заданному быстродействию и устойчивости;