Системы автоматической стабилизации того или иного технологического параметра. Системы автоматического регулирования с запаздыванием, страница 13

от величины максимального пика ВЧХ, т.е. графиками и  (Рис. 16 ) [ 7]. Из этих графиков по заданным величинам  и  определяем частоту среза желаемой ЛАХ:

          (2.10)

и величину . Значение минимума ВЧХ принимаем

.       (2.11)

Если, например, задано  и , то из рис. 16 и уравнений (2.10) и (2.11) находим ; ; .

Для того чтобы выполнялось условие , необходимо на номограмме для  (рис. 17) построить запретную область в виде прямоугольника, стороны которого являются касательными к кривым с индексами  и . Из запретной зоны легко определить требуемые превышения, по модулю  и  и запасы по фазе  и .

Так, при =1.2 и =--0,2 находим =15дБ, =-15дБ;. Откладывая на оси частот полученную по уравнению (2.10) величину  для желаемой ЛАХ, проводим через эту точку прямую с наклоном -20 дБ/дек. Протяженность этой прямой  занимает диапазон частот, в котором выполняется условие . Сопряжение среднечастотной части желаемой ЛАХ с низкочастотной и высокочастотной частью неизменяемой ЛАХ выполняется прямыми, наклоны которых отличаются как можно меньше от соответствующих наклонов неизменяемой ЛАХ. При этом корректирующие устройства получаются наиболее простыми.

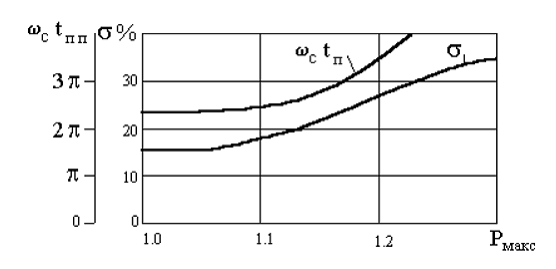
Рис. 16. Зависимость перерегулирования и относительного времени переходного процесса от максимального значения ВЧХ замкнутой системы.

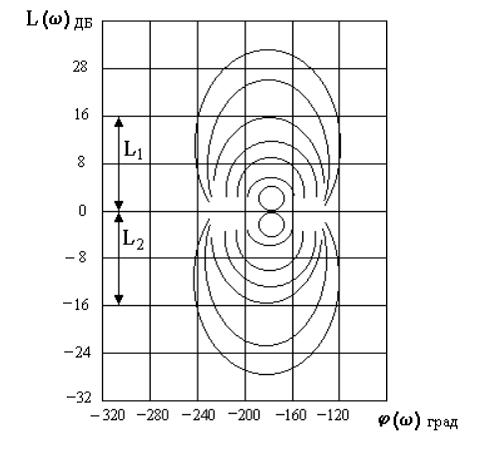
Рис. 17. Номограммы для определения запасов по модулю и фазы.

Пример 2.

Задана передаточная функция разомкнутой нескорректированной следящей системы:

.

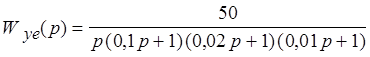Сформировать желаемую ЛАХ, если известно, что максимальная ошибкане должна превышать  при скорости вращения задающей оси =18 град/с. Момент сопротивления нагрузки = 4 10⁴ г.см, передаточное число редуктора =100, жесткостъ механических характеристик двигателя  =2 г.см.с/град,  время переходного процесса , перерегулирование .

Решение.

1. Из табл. 6 определим требуемый коэффициент усиления разомкнутой системы, обеспечивающий заданную точность в установившемся режиме:

.

2. Построим ЛАХ нескорректированной исходной системы, для чего на частоте  отложим  и проведем через эту точку асимптоту с наклоном -20 дБ/дек до первой сопряженной частоты, затем прямую с наклоном -40дБ/дек до следующей сопряженной частоты, изменим наклон на -60дБ/дек и, наконец, с частоты 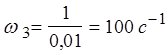 проводим высокочастотную асимптоту с наклоном -80 дБ/дек.

Таким образом, ЛАХ исходной системы  имеет вид 1-2-3-4  (рис. 18 ).

3.Построим желаемую ЛАХ. Для этого по графикам рис. 16 находим =1.2; =-0.2; 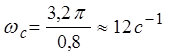,а по номограмме рис.17 определяем =15 дБ, =-15 дБ. Исходя из простоты корректирующего устройства уменьшаем  до -12дБ. Среднечастотную часть желаемой ЛАХ строим в виде прямой с наклоном -20 дБ/дек, проходящей через точку  и расположенной в диапазоне частот от до. В низкочастотной части сопряжение и  осуществим прямой с наклоном -40дБ/дек. В высокочастотной части, начиная с частоты ,

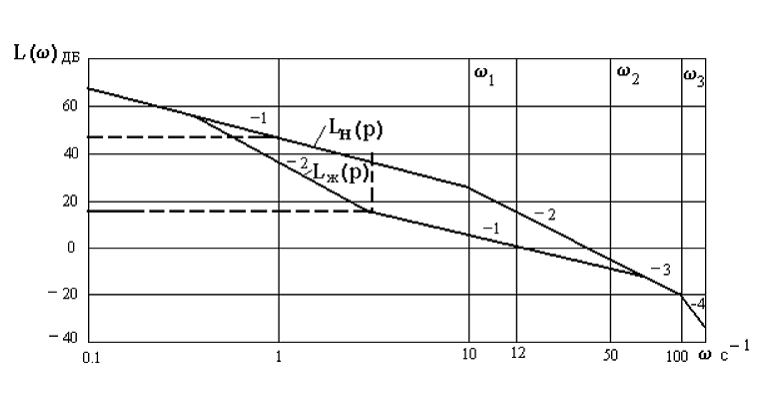
Рис. 18. Формирование желаемой ЛАХ по методу Солодовникова.

ЛАХ желаемой САР совпадает с ЛАХ исходной системы.

3. Методика Е. А. Санковского (третий тип задания)

По этой методике желаемые ЛАХ характеризуются отношением наклонов второй низкочастотной асимптоты и первой  и вводят в рассмотрение параметр

.

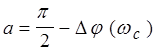Для самой распространенной желаемой ЛАХ (тип - -2/1) получают следующие соотношения:

; ;

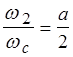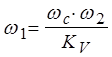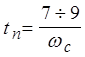; , которые позволяют полностью сформировать желаемую ЛАХ. Подробные примеры на построение желаемой ЛАХ по этой методике приведены в [8].

Учет воздействия помех

В некоторых вариантах курсового проекта в качестве исходных данных задаются спектральная плотность широкополосной помехи типа белый шум  и дисперсия допустимой флюктуационной ошибки . Эти требования, необходимо учитывать при формировании желаемой ЛАХ.

Вычисляя  допустимую полосу шумов по выражению  и используя приближенное соотношение

или

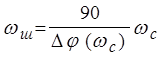, определяют предельное верхнее значение частоты среза .

Если ограничена полная среднеквадратическая ошибка системы, то следует иметь в виду, что

, где  - динамическая ошибка.

Выбор способа включения корректирующего устройства